Not a Free Lunch But a Box of Chocolates

A critique of William Dembski's book No Free Lunch

By Richard Wein

Life is like a box of chocolates. You never know what you're gonna get.
Forrest Gump

The aim of Dr William Dembski's book No Free Lunch is to demonstrate that design (the action of a conscious agent) was involved in the process of biological evolution. The following critique shows that his arguments are deeply flawed and have little to contribute to science or mathematics. To fully address Dembski's arguments has required a lengthy and sometimes technical article, so this summary is provided for the benefit of readers without the time to consider the arguments in full.

Dembski has proposed a method of inference which, he claims, is a rigorous formulation of how we ordinarily recognize design. If we can show that an observed event or object has low probability of occurring under all the non-design hypotheses (explanations) we can think of, Dembski tells us to infer design. This method is purely eliminative--we are to infer design when we have rejected all the other hypotheses we can think of--and is commonly known as an argument from ignorance, or god-of-the-gaps argument.

Because god-of-the-gaps arguments are almost universally recognized by scientists and philosophers of science to be invalid as scientific inferences, Dembski goes to great length to disguise the nature of his method. For example, he inserts a middleman called specified complexity: after rejecting all the non-design hypotheses we can think of, he tells us to infer that the object in question exhibits specified complexity, and then claims that specified complexity is a reliable indicator of design.

The only biological object to which Dembski applies his method is the flagellum of the bacterium E. coli. First, he attempts to show that the flagellum could not have arisen by Darwinian evolution, appealing to a modified version of Michael Behe's argument from irreducible complexity. However Dembski's argument suffers from the same fundamental flaw as Behe's: he fails to allow for changes in the function of a biological system as it evolves.

Since Dembski's method is supposed to be based on probability and he has promised readers of his earlier work a probability calculation, he proceeds to calculate a probability for the origin of the flagellum. But this calculation is based on the assumption that the flagellum arose suddenly, as an utterly random combination of proteins. The calculation is elaborate but totally irrelevant, since no evolutionary biologist proposes that complex biological systems appeared in this way. In fact, this is the same straw man assumption frequently made by Creationists in the past, and which has been likened to a Boeing 747 being assembled by a tornado blowing through a junkyard.

This is all there is to Dembski's main argument. He then makes a secondary argument in which he attempts to show that even if complex biological systems did evolve by undirected evolution, they could have only done so if a designer had fine-tuned the fitness function or inserted complex specified information at the start of the process.

The argument from fine-tuning of fitness functions appeals to a set of mathematical theorems called the "No Free Lunch" theorems. Although these theorems are perfectly sound, they do not have the implications which Dembski attributes to them. In fact they do not apply to biological evolution at all. All that is left of Dembski's argument is then the claim that life could only have evolved if the initial conditions of the Universe and the Earth were finely tuned for that purpose. This is an old argument, usually known as the argument from cosmological (and terrestrial) fine-tuning. Dembski has added nothing new to it.

Complex specified information (CSI) is a concept of Dembski's own invention which is quite different from any form of information used by information theorists. Indeed, Dembski himself has berated his critics in the past for confusing CSI with other forms of information. This critique shows that CSI is equivocally defined and fails to characterize complex structures in the way that Dembski claims it does. On the basis of this flawed concept, he boldly proposes a new Law of Conservation of Information, which is shown here to be utterly baseless.

Dembski claims to have made major contributions to the fields of statistics, information theory and thermodynamics. Yet his work has not been accepted by any experts in those fields, and has not been published in any relevant scholarly journals.

No Free Lunch consists of a collection of tired old antievolutionist arguments: god-of-the-gaps, irreducible complexity, tornado in a junkyard, and cosmological fine-tuning. Dembski attempts to give these old arguments a new lease of life by concealing them behind veils of confusing terminology and unnecessary mathematical notation. The standard of scholarship is abysmally low, and the book is best regarded as pseudoscientific rhetoric aimed at an unwary public which may mistake Dembski's mathematical mumbo jumbo for academic erudition.

1. Introduction

In the theater of confusion, knowing the location of the exits is what counts.
Mason Cooley, U.S. aphorist

William Dembski's book No Free Lunch: Why Specified Complexity Cannot be Purchased without Intelligence¹ is the latest of his many books and articles on inferring design in biology, and will probably play a central role in the promotion of Intelligent Design pseudoscience² over the next few years. It is the most comprehensive exposition of his arguments to date. The purpose of the current critique is to provide a thorough critical examination of these arguments. Dembski himself has often complained that his critics have not fully engaged his arguments. I believe that complaint is unjustified, though I would agree that some earlier criticisms have been poorly aimed. This critique should lay to rest any such complaints.

As in his previous work, Dembski defines his own terms poorly, gives new meanings to existing terms (usually without warning), and employs many of these terms equivocally. His assertions often appear to contradict one another. He introduces a great deal of unnecessary mathematical notation. Thus, much of this article will be taken up with the rather tedious chore of establishing just what Dembski's arguments and claims really mean. I have tried very hard to find charitable interpretations, but there are often none to be found. I have also requested clarifications from Dembski himself, but none have been forthcoming.

Some time ago, I posted a critique³ of Dembski's earlier book, The Design Inference,⁴ to the online Metaviews forum, to which he contributes, pointing out the fundamental ambiguities in his arguments. His only response was to call me an "Internet stalker" while refusing to address the issues I raised, on the grounds that "the Internet is an unreliable forum for settling technical issues in statistics and the philosophy of science".⁵ He clearly read my critique, however, since he now acknowledges me as having contributed to his work (p. xxiv). While some of the ambiguities I drew attention to in that earlier critique have been resolved in his present volume, others have remained and many new ones have been added.

Some readers may dislike the frankly contemptuous tone that I have adopted towards Dembski's work. Critics of Intelligent Design pseudoscience are faced with a dilemma. If they discuss it in polite, academic terms, the Intelligent Design propagandists use this as evidence that their arguments are receiving serious attention from scholars, suggesting this implies there must be some merit in their arguments. If critics simply ignore Intelligent Design arguments, the propagandists imply this is because critics cannot answer them. My solution to this dilemma is to thoroughly refute the arguments, while making it clear that I do so without according those arguments any respect at all.

This critique assumes a basic knowledge of mathematics, probability theory and evolutionary theory on the part of the reader. In order to simplify some of my arguments, I have relegated many details to endnotes, which can be reached by numbered links. In some cases, assertions which are not substantiated in the body of the text are supported by arguments in endnotes.

Citations consisting merely of page numbers refer to pages in No Free Lunch.

Regrettably, some older browsers are unable to display a number of mathematical symbols which are used in this article. Netscape 4 is one of these.

2. Design and Nature

In spring, when woods are getting green,
I'll try and tell you what I mean.
Lewis Carroll, Through the Looking-Glass (Humpty Dumpty)

For a book which is all about inferring design, it is surprising to discover that No Free Lunch does not clearly define the term. Design is equated with intelligent agency, but that term is not defined either. It is also described negatively, as the complement of necessity (deterministic processes) and chance (stochastic processes). However, deterministic and stochastic processes are themselves normally defined as mutually exhaustive complements: those processes which do not involve any uncertainty and those which do. So it is not clear what, if anything, remains after the exclusion of those two categories. Dembski associates design with the actions of animals, human beings and deities, but seems to deny the label to the actions of computers, no matter how innovative their output may be. What distinguishes an animal mind, say, from a computer? Obviously there are many physical differences. But why should the actions of one be considered design and not the other? The only explanation I can think of is that one is conscious and the other, presumably, is not. I conclude that, when he infers design, Dembski means that a conscious mind was involved.

It appears that Dembski considers consciousness to be a very special kind of process, which cannot be attributed to physical laws. He tells us that intelligent design is not a mechanistic explanation (pp. 330-331). Dembski would certainly not be alone in this view, though it is not at all clear what it means for a process to be non-mechanistic. It appears, however, that such a process is outside the realm of cause and effect. This raises all sorts of difficult philosophical questions, which I will not attempt to consider here. Even if we accept that non-mechanistic processes exist, Dembski gives us no reason to think that consciousness (or intelligent design) is the only possible type of non-mechanistic process. Yet he seems to assume this to be the case.

Even with this interpretation, we still run into a problem. In his Caputo example (p. 55), Dembski uses his design inference to distinguish between two possible explanations both involving the actions of a conscious being: either Caputo drew the ballots fairly or he cheated. Dembski considers only the second of these alternatives to be design. But both explanations involve a conscious agent. It could be said that, if Caputo drew fairly, he was merely mimicking the action of a mechanistic device, so this doesn't count. But that would raise the question of just what a mechanistic device is capable of doing. Is a sophisticated computer not capable of cheating? Indeed, is there any action of a human mind which cannot, in principle, be mimicked by a sufficiently sophisticated computer? If not, how can we tell the difference between conscious design and a computer mimicking design? Even if you doubt that in principle a computer could mimic all the actions of a human mind, consider whether it could mimic the actions of a rat, which Dembski also considers to be an intelligent agent capable of design (pp. 29-30).

To escape this dilemma, Dembski invokes the concept of derived intentionality: the output of a computer can "exhibit design", but the design was performed by the creator of the computer and not by the computer itself (pp. 223, 326). Whenever a phenomenon exhibits design, there must be a designer (a conscious mind, in my interpretation) somewhere in the causal chain of events leading to that phenomenon.

Dembski claims that contemporary science rejects design as a legitimate mode of explanation (p. 3). But he himself gives examples of scientists making inferences involving human agency, such as the inference by archaeologists that certain stones are arrowheads made by early humans (p. 71), and he labels these "design inferences". Is he claiming that such archaeologists are mavericks operating outside the bounds of mainstream science? I don't think so. I think that what Dembski really means to claim here is that contemporary science does not allow explanations involving non-mechanistic processes, and he is projecting his own belief that design is a non-mechanistic process onto contemporary science. But even if it's true that science does not allow explanations involving non-mechanistic processes, it certainly does allow the action of a mind to be inferred where no judgement need be made as to whether mental processes are mechanistic or not (and such a judgement is generally unnecessary).

An alternative interpretation of Dembski's claim might be that contemporary science rejects design as a legitimate mode of explanation in accounting for the origin of biological organisms. If this is what he means, then I reject the claim. If we were to discover the remains of an ancient alien civilization with detailed records of how the aliens manipulated the evolution of organisms, then I think that mainstream science would have little difficulty accepting this as evidence of design in biological organisms.

The word natural has been the source of much confusion in the debate over Intelligent Design. It has two distinct meanings: one is the complement of artificial, i.e. involving intelligent agency; the other is the complement of supernatural. Dembski tells us that he will use the word in the former sense: "...I am placing natural causes in contradistinction to intelligent causes" (p. xiii). He then goes on to say that contemporary science is wedded to a principle of methodological naturalism:

According to methodological naturalism, in explaining any natural phenomenon, the natural sciences are permitted to invoke only natural causes to the exclusion of intelligent causes. [p. xvi]

But the methodological naturalism on which most scientists insist requires only the rejection of supernatural explanations, not explanations involving intelligent agency. Indeed, we have just seen that contemporary science allows explanations involving human designers and, I argue, intelligent alien beings. Perhaps what Dembski really means is that methodological naturalism rejects the invocation of an "unembodied designer" (to use his term).⁶

Dembski introduces the term chance hypothesis to describe proposed explanations which rely entirely on natural causes. This includes processes comprising elements of both chance and necessity (p.15), as well as purely deterministic processes. It may seem odd to refer to purely deterministic hypotheses as chance hypotheses, but Dembski tells us that "necessity can be viewed as a special case of chance in which the probability distribution governing necessity collapses all probabilities either to zero or one" (p.71). Since Dembski defines design as the complement of chance and necessity, it follows that a chance hypothesis could equally well (and with greater clarity) be called a non-design hypothesis. And since he defines natural causes as the complement of design, we can also refer to chance hypotheses as natural hypotheses. Dembski's use of the term chance hypothesis has caused considerable confusion in the past, as many people have taken chance to mean purely random, i.e. all outcomes being equally probable. While Dembski's usage has been clarified in No Free Lunch, I believe it still has the potential to confuse. For the sake of consistency with Dembski's work, I will generally use the term chance hypothesis, but I will switch to the synonym natural hypothesis or non-design hypothesis when I think this will increase clarity.

3. The Chance-Elimination Method

Ignorance, Madam, pure ignorance.
Samuel Johnson (on being asked how he came to define a word incorrectly in his dictionary)

In Chapter 2 of No Free Lunch, Dembski describes a method of inferring design based on what he calls the Generic Chance Elimination Argument. I'll refer to this method as the chance-elimination method. This method assumes that we have observed an event, and wish to determine whether any design was involved in that event.

The chance-elimination method is eliminative--it relies on rejecting chance hypotheses. Dembski gives two methods for eliminating chance hypotheses: a statistical method for eliminating individual chance hypotheses, and proscriptive generalizations, for eliminating whole categories of chance hypotheses.

3.1 Dembski's Statistical Method

The fundamental intuition behind Dembski's statistical method is this: we have observed a particular event (outcome) E and wish to check whether a given chance hypothesis H provides a reasonable explanation for this outcome.⁷ We select an appropriate rejection region (a set of potential outcomes) R, where E is in R, and calculate the probability of observing an outcome in this rejection region given that H is true, i.e. P(R|H). If P(R|H) < α, where α is an appropriate small probability bound, we consider it implausible that an event of such small probability could have occurred, and so we reject the chance hypothesis H which gave rise to this small probability.

It is important to note that we need to combine the probabilities of all outcomes in an appropriate rejection region, and not just take the probability of the particular outcome observed, because outcomes can individually have small probabilities without their occurrence being significant. A rejection region which is appropriate for use in this way is said to be detachable from the observed outcome, and a description of a detachable rejection region is called a specification (though Dembski often uses the terms rejection region and specification interchangeably).

Consider Dembski's favourite example, the Caputo case (pp. 55-58). A Democrat politician, Nicholas Caputo, was responsible for making random draws to determine the order in which the two parties (Democrat and Republican) would be listed on ballot papers. Occupying the top place on the ballot paper was known to give the party an advantage in the election, and it was observed that in 40 out of 41 draws Caputo drew a Democrat to occupy this favoured position. In 1985 it was alleged that Caputo had deliberately manipulated the draws in order to give his own party an unfair advantage. The court which considered the allegation against Caputo noted that the probability of picking his own party 40 out of 41 times was less than 1 in 50 billion, and concluded that "confronted with these odds, few persons of reason will accept the explanation of blind chance."⁸

In conducting his own analysis of this event, Dembski arrives at the same probability as did the court, and explains the reasoning behind his conclusion. The chance hypothesis H which he considers is that Caputo made the draws fairly, with each party (D and R) having a 1/2 probability of being selected for the top place on each occasion.

Suppose that we had observed a typical sequence of 41 draws, such as the following:

DRRDRDRRDDDRDRDDRDRRDRRDRRRDRRRDRDDDRDRDD

The probability of this precise sequence occurring, given H, is extremely small: (1/2)⁴¹ = 4.55 × 10^-13. However, unless that particular sequence had been predicted in advance, we would not consider the outcome at all exceptional, despite its low probability, since it was very likely that some such random looking sequence would occur. The historical sequence, on the other hand, contained just one R, and so looked something like this:

DDDDDDDDDDDDDDDDDDDDDDRDDDDDDDDDDDDDDDDDD

The second sequence (call it E) has exactly the same probability as the first one, i.e. P(E|H) = 4.55 × 10^-13, but this time we would consider it exceptional, because the probability of observing so many Ds is extremely small. Any outcome showing as many Ds as this (40 or more Ds out of 41 draws) would have been considered at least as exceptional, so the probability we are interested in is the probability of observing 40 or more Ds. "40 or more Ds", then, is our specification, and, as it happens, there are 42 different sequences matching this specification, so P(R|H) = 42 × P(E|H) = 1.91 × 10^-11, or about 1 in 50 billion. In other words, the probability we are interested in here is not the probability of the exact sequence we observed, but the probability of observing some outcome matching the specification. If we decide that this probability is small enough, we reject H, i.e. we infer that Caputo's draws were not fair. From now on, I will use the expression "small probability" to mean "probability below an appropriate probability bound".

In order to apply Dembski's method, we need to know how to select an appropriate specification and probability bound. Dembski expounds at length a set rules for selecting these parameters, but they can be boiled down to the following:

• An appropriate specification is merely any one which can be derived (in some loose sense) from background knowledge which was available to us before observing the event in question. For example, when Dembski applies his method to the bacterial flagellum--his only biological example--he doesn't bother to use the technical rules that he developed earlier, or even to state the specification explicitly. Reading between the lines, his specification appears to be "anything with the function of an outboard rotary motor", and the only justification he gives for this specification is the statement that "humans developed outboard rotary motors well before they figured out that the flagellum was such a machine" (p. 289).

• Dembski distinguishes between local and universal probability bounds. A local probability bound is one which is calculated for the purpose of a particular statistical test.⁹ The procedure for calculating such a bound is difficult and highly arbitrary (p. 83), so Dembski generally falls back on his universal probability bound. This is a very small number, 10^-150 (i.e. 1 in 10¹⁵⁰), which Dembski tells us is the smallest probability bound we need ever use, and which we can always use in the absence of a suitable local probability bound. He calculates it by multiplying the number of elementary particles in the Universe, the maximum possible number of elementary particle transitions (the inverse of the Planck time) per second, and the number of seconds in a billion times the current age of the Universe, to give a figure which, he argues, is the maximum number of probabilistic resources we need ever consider (p. 22):

  10⁸⁰ × 10⁴⁵ × 10²⁵ = 10¹⁵⁰

Although I believe Dembski's statistical method is seriously flawed, the issue is not important to my refutation of Dembski's design inference. For the remainder of the main body of this critique, therefore, I will assume for the sake of argument that the method is valid. A discussion of the flaws will be left to an appendix. It is worth noting, however, that this method has not been published in any professional journal of statistics and appears not to have been recognized by any other statistician.

3.2 Proscriptive Generalizations

Dembski argues that we can eliminate whole categories of chance hypotheses by means of proscriptive generalizations. For example, he mentions the second law of thermodynamics, which proscribes the possibility of a perpetual motion machine. He describes the logic of such generalizations in terms of mathematical invariants (p. 274), though this adds absolutely nothing to his argument.

I accept that proscriptive generalizations can sometimes be made, and Dembski is welcome to use them to eliminate specific categories of chance hypotheses. But there is no proscriptive generalization that can rule out all chance hypotheses. Furthermore, his claim to have found a proscriptive generalization against Darwinian evolution of irreducibly complex systems is hollow (see 4.2 below).

3.3 The Argument From Ignorance

The conclusion of the Generic Chance Elimination Argument (step #8) is stated by Dembski as follows:

S [the subject making the inference] is warranted in inferring that E [the observed outcome] did not occur according to any of the chance hypotheses in {H_i}_{i in I} and therefore that E exhibits specified complexity. [p. 73]

{H_i} is the set of all chance hypotheses which we believe "could have been operating to produce E" (p.72). Dembski also writes:

But what happens once some causal mechanism is found that accounts for a given instance of specified complexity? Something that is specified and complex is highly improbable with respect to all causal mechanisms currently known. Consequently, for a causal mechanism to come along and explain something that previously was regarded as specified and complex means that the item in question is in fact no longer specified and complex with respect to the newly found causal mechanism. [p. 330]

So, when we have eliminated all the chance hypotheses we can think of, we infer that the event was highly improbable with respect to all known causal mechanisms, and we call this specified complexity. Later Dembski tells us that an inference of specified complexity should lead inevitably to an inference of design. This being the case, it's not clear that the notion of specified complexity is serving any useful purpose here. Why not cut out the middleman and go straight from the Generic Chance Elimination Argument to design? Unfortunately, the introduction of this middleman does serve to cause considerable confusion, because Dembski equivocates between this sense of specified complexity and the sense assigned by his uniform-probability method of inference (which I will explain in section 6). To help clear up the confusion, I will refer to this middleman sense as eliminative specified complexity and to the other sense as uniform-probability specified complexity. Note that Dembski's specified complexity is not a quantity: an event simply exhibits specified complexity or it doesn't.

Thus we see that the chance-elimination method is purely eliminative. It tells us to infer design when we have ruled out all the chance (i.e. non-design) hypotheses we can think of. The design hypothesis says nothing whatsoever about the identity, nature, aims, capabilities or methods of the designer. It just says, in effect, "a designer did it".¹⁰

This type of argument is commonly known as an argument from ignorance or god-of-the-gaps argument. So there is no danger of misunderstanding, let me clarify that the accusation of argument from ignorance is not an assertion that those making the argument are ignorant of the facts, or even that they are failing to utilize the available facts. The proponents of an argument from ignorance are demanding that their explanation be accepted just because the scientific community is ignorant (at least partially) of how an event occurred, rather than because their own explanation has been shown to be a good one. Note that an argument from scientific ignorance differs from the deductive fallacy of argument from ignorance. The deductive fallacy takes the following form: "My proposition has not been proven false, so it must be true." The scientific argument from ignorance is not a deductive fallacy, because scientific inferences are not deductive arguments.

A god-of-the-gaps argument is an argument from ignorance in which the default hypothesis, to be accepted when no alternative hypothesis is available, is "God did it". Since Dembski tells us that his criterion only infers the action of an unknown designer, and not necessarily a divine one, the term designer-of-the-gaps might be more appropriate here, but I think it is reasonable to use the more familiar term, since the arguments follow the same eliminative pattern and Dembski has made it clear that the designer he has in mind is the Christian God. The god-of-the-gaps argument should not be confused with a god-of-the-gaps theology. The latter proposes that God's actions are restricted to those areas of which we lack knowledge, but does not offer this as an argument for the existence of God.

Dembski makes no good case for awarding such a privileged status to the design hypothesis. Why should we prefer "an unknown designer did it" to "unknown natural causes did it" or "we don't know what did it"? Furthermore, as we shall see, he tells us to accept design by elimination even when we do have some outline ideas for how natural causes might have done it.

3.4 Dembski's Responses to the Charge of Argument From Ignorance

Since arguments from ignorance are almost universally rejected as unsound by scientists and philosophers of science, Dembski is sensitive to the charge, but his attempts to avoid facing up to the obvious are mere evasions.

In response to this criticism, note first that even though specified complexity is established via an eliminative argument, it is not fair to say that it is established via a purely eliminative argument. If the argument were purely eliminative, one might be justified in saying that the move from specified complexity to a designing intelligence is an argument from ignorance (i.e., not X therefore Y). But unlike Fisher's approach to hypothesis testing, in which individual chance hypotheses get eliminated without reference to the entire set of relevant chance hypotheses that might explain a phenomenon, specified complexity presupposes that the entire set of relevant chance hypotheses has first been identified. This takes considerable background knowledge. What's more, it takes considerable background knowledge to come up with the right pattern (i.e., specification) for eliminating all those chance hypotheses and thus for inferring design. [p. 111]

Dembski is misconstruing the charge of argument from ignorance. It is not a question of how much knowledge we have utilized. Scientific knowledge is always incomplete. The chance-elimination method is purely eliminative because it makes no attempt to consider the merits of the design hypothesis, but merely relies on eliminating the available alternatives.

Design inferences that infer design by identifying specified complexity are therefore not purely eliminative. They do not merely exclude, but they exclude from an exhaustive set in which design is all that remains once the inference has done its work (which is not to say that the set is logically exhaustive; rather, it is exhaustive with respect to the inquiry in question--that is all we can ever do in science). Design inferences, by identifying specified complexity, exclude everything that might in turn exclude design. [p. 111]

Dembski's phrase "exhaustive with respect to the inquiry in question" is the sort of circumlocution in which he excels. It just means that the set is as exhaustive as we can make it. In other words, it's a fancy way to say we have eliminated all the chance hypotheses we could think of.

Design inferences therefore eliminate chance in the global sense of closing the door to all relevant chance explanations. To be sure, this cannot be done with absolute finality since there is always the possibility that some crucial probability distribution was missed. Nonetheless, it is not enough for the design skeptic merely to note that adding a new chance explanation to the mix can upset a design inference. Instead, the design skeptic needs to explicitly propose a new chance explanation and argue for its relevance to the case at hand. [pp. 67-68]

This is a clear argument from ignorance. Unless design skeptics can propose an explicit natural explanation, Dembski tells us, we should infer design.

For any event whatsoever, there exists a probability distribution that concentrates all probability on that event and thus assigns it a probability of one. It therefore makes no sense to criticize my generalization of Fisher's approach to hypothesis testing for failing to consider all possible chance hypotheses. [p. 70]

Dembski is not being criticized for failing to eliminate all possible chance hypotheses, but for adopting a purely eliminative method in the first place.

Archeologists infer that certain chunks of rock are arrowheads. Detectives infer that certain deaths were deliberate. Cryptographers infer that certain random looking symbol strings are actually encrypted messages. In every case they might be wrong, and further knowledge might reveal a plausible chance hypothesis behind what originally appeared to be designed. But such sheer possibilities by themselves do nothing to overturn our confidence in design inferences. [p. 71]

Yes, these design inferences are fallible, as are all scientific inferences. That is not the issue. The difference is that these inferences are not purely eliminative. The experts in question have in mind a particular type of intelligent designer (human beings) of which they know much about the abilities and motivations. They can therefore compare the merits of such an explanation with the merits of other explanations.

If Dembski wishes to defend god-of-the-gaps arguments as a legitimate mode of scientific inference, he is welcome to try. What is less welcome are his attempts to disguise his method as something more palatable.

3.5 Comparative and Eliminative Inferences

One way in which Dembski attempts to defend his method is to suggest that there is no viable alternative. The obvious alternative, however, is to consider all available hypotheses, including design hypotheses, on their merits, and then select the best of them. This is the position adopted by almost all philosophers of science, although they disagree on how to evaluate the merits of hypotheses. There seems no reason to treat inferences involving intelligent agents differently in this respect from other scientific inferences.

Dembski argues at some length against the legitimacy of comparative approaches to inference (pp. 101-110, 121n59). I will not address the specifics of the likelihood approach, on which he concentrates his fire. I leave that to its proponents. However, his rejection of comparative inferences altogether is clearly untenable. When we have two or more plausible hypotheses available--whether those involve intelligent agents or not--we must use some comparative method to decide between them.

Consider, for example, the case of the archaeologists who make inferences about whether flints are arrowheads made by early humans or naturally occurring pieces of rock. Let us take a borderline case, in which a panel of archaeologists is divided about whether a given flint, taken from a site inhabited by early humans, is an arrowhead. Now suppose that the same panel had been shown the same flint but told that it came from a location which has never been inhabited by flint-using humans, say Antarctica. The archaeologists would now be much more inclined to doubt that the flint was man-made, and more inclined to attribute it to natural causes. A smaller proportion (perhaps none at all) would now infer design. The inference of design, then, was clearly influenced by factors affecting the plausibility of the design hypothesis: whether or not flint-using humans were known to have lived in the area. The inference was not based solely on the elimination of natural hypotheses.

It is not my intention to argue for any particular method of comparing hypotheses. Philosophers of science have proposed a number of comparative approaches, usually involving some combination of the following criteria:

• Likelihood. The probability of the evidence occurring given the hypothesis in question.
• Prior probability or plausibility. Our degree of belief in the hypothesis prior to observing the evidence, or assuming we had not observed it.
• Predictive power. The degree to which the hypothesis determines which potential observations are possible (or probable) and which are impossible (or improbable).
• Falsifiability. The degree to which the hypothesis "risks" being falsified by new evidence.
• Parsimony. The degree to which the hypothesis observes the principle of Occam's razor: "Do not multiply entities needlessly."¹¹

Other criteria often cited include explanatory power, track record, scope, coherence and elegance.

In opposing comparative methods, Dembski argues that hypotheses can be eliminated in isolation without there necessarily being a superior competitor. In practical terms, I agree, although I suspect that we would not eliminate a hypothesis unless we had in the back of our minds that there existed a plausible possibility of a better explanation. I do not deny that we can eliminate a hypothesis without having a better one in mind; I deny that we can accept a hypothesis without having considered its merits, as Dembski would have us do in the case of his design hypothesis. If all the available hypotheses score too badly according to our criteria, it may be best to reject all of them and just say "we don't know".

3.6 Reliability and Counterexamples

Dembski argues, on the basis of an inductive inference, that the chance-elimination method is reliable:

First (section 1.6) I offered an inductive argument, showing that in all cases where we know the causal history and where specified complexity was involved, an intelligence was involved as well. The inductive generalization that follows is that all cases of specified complexity involve intelligence. [p. 110]

Setting aside the question of whether such an induction would be justified if its premise were true, let's just consider whether or not the premise is true. Contrary to Dembski's assertion, his section 1.6 did not show anything of the sort. In fact, the only cases where we know that Dembski's method has been used to infer design are the two examples that Dembski himself describes: the Caputo case and the bacterial flagellum. And in neither of these cases has design been independently established.

Dembski wants us to believe that his method of inference is basically the same method already used in our everyday and scientific inferences of design. I have already argued that this is untrue. But even if we suppose, for the sake of argument, that our typical design inferences are indeed based on the sort of purely eliminative approach proposed by Dembski, then it is not difficult to find counterexamples, in which design was wrongly inferred because of ignorance of the true natural cause:

• Fairy rings. These are rings of mushrooms caused by a fungus spreading through grass at a uniform rate from a given starting point. Mushrooms are manifested on the outer rim of the affected circle. Before the cause was known, these rings were often attributed to intelligent designers ("fairies"). If we take the chance hypothesis that the mushrooms were randomly located throughout a meadow (with a uniform probability distribution), the probability of them forming a neat circle is clearly small enough to justify the rejection of this hypothesis (by use of an appropriate local probability bound, if not Dembski's universal probability bound).¹² Using Dembski's chance-elimination method, specified complexity (and hence design) would have been inferred erroneously.

• Moon craters. On observing the major craters of the Moon, Johannes Kepler concluded that they were too circular to have occurred by chance, and so must have been created by inhabitants of the Moon. If we take the chance hypothesis that the craters were formed out of many individual hills, and that these hills were randomly distributed across the surface of the Moon, then the probability of them forming such good circles is clearly small enough to reject this hypothesis. Using Dembski's chance-elimination method, specified complexity (and hence design) would have been inferred, but we now know that these craters have a natural explanation--impacts from falling objects. I am indebted for this example to Dembski himself, who describes it¹³ but fails to notice that it provides a counterexample to his claim.

Perhaps Dembski would object that his claim ("in all cases where we know the causal history and where specified complexity was involved, an intelligence was involved as well") was only referring to cases where we observe specified complexity today. But, by definition, those are cases where we don't have a plausible natural explanation. If we had one, we would not infer specified complexity. If we know the causal history and it was not a natural cause, it must have been design. So, if this is what Dembski means, his claim is a tautology. It says that, whenever the cause is known to be design, the cause is design! You cannot make an inductive inference from a tautology.

It would do Dembski no good to claim that these are cases of derived design (see 6.1 below), e.g. that mushrooms and the solar system were originally designed. The chance-elimination method infers design in the particular event which is alleged to have small probability of occurring under natural causes. For example, in the case of the flagellum, Dembski claims that design was involved in the origin of the flagellum itself, and not just indirectly in terms of the Earth or the Universe having been designed.

3.7 The Explanatory Filter

The chance-elimination method is initially introduced in a simplified form called the Explanatory Filter. The criterion for the filter to recognize design is labelled the complexity-specification criterion. Unfortunately, the use of this simplified account has caused considerable confusion in the past, because it possesses two misleading features:

• The description of the Explanatory Filter hardly mentions the concept of chance hypotheses, and implies that we need consider only one probability distribution. The flow chart for the filter (p. 13) should contain a loop, to be executed for each chance hypothesis. Many readers of Dembski's past work have been led to the erroneous conclusion that we only need to calculate the probability with respect to a uniform probability distribution.

• The Explanatory Filter has separate nodes for complexity (which Dembski uses here as a synonym for improbability) followed by specification, as if these were two separate criteria. But, as we saw above, we cannot calculate the probability until we have formulated a specification. Many of Dembski's readers in the past have erroneously interpreted the filter as follows: note that the observed outcome is specified (in some sense) and then calculate the probability of that single outcome (when they should have calculated the probability of an entire rejection region).

Although Dembski has made some attempts to clarify the situation in No Free Lunch, his continued use of the Explanatory Filter in its highly misleading form is inexplicable. And the misdirection is not limited to the Explanatory Filter itself. It occurs elsewhere too, in statements such as this:

Determining whether an irreducibly complex system exhibits specified complexity involves two things: showing that the system is specified and calculating its probability... [p. 289]

4. Applying the Method to Nature

He uses statistics as a drunken man uses lampposts--for support rather than illumination.
Andrew Lang (1844-1912), poet and novelist

4.1 A Tornado in a Junkyard

It has been several years since Dembski first claimed to have detected design in biology by applying his method of inference. Yet until the publication of No Free Lunch, he had never provided or cited the details of any such application. Critics were therefore looking forward to seeing the long-promised probability calculation that would support the claim. While I, for one, did not expect a convincing calculation, even I was amazed to discover that Dembski has offered us nothing but a variant on the old Creationist "tornado in a junkyard"¹⁴ straw man, namely the probability of a biological structure occurring by purely random combination of components.

The only biological structure to which Dembski applies his method is the flagellum of the bacterium E. coli. As his method requires him to start by determining the set {H_i}of all chance hypotheses which "could have been operating to produce E [the observed outcome]" (p. 72), one might expect an explicit identification of the chance hypothesis under consideration. Dembski provides no such explicit identification, and the reader is left to infer it from the details of the calculation. Perhaps the reason Dembski failed to identify his chance hypothesis is that, when clearly named, it is so transparently a straw man. No biologist proposes that the flagellum appeared by purely random combination of proteins--they believe it evolved by natural selection--and all would agree that the probability of appearance by random combination is so minuscule that this is unsatisfying as a scientific explanation. Therefore for Dembski to provide a probability calculation based on this absurd scenario is a waste of time. There is no need to consider whether Dembski's calculation is correct, because it is totally irrelevant to the issue. Nevertheless, since Dembski does not state clearly that he has based his calculation on a hypothesis of purely random combination, I will describe the calculation briefly in order to demonstrate that this is the case.

Dembski tells us to multiply three partial probabilities to arrive at the probability of a "discrete combinatorial object":

p_dco = p_orig × p_local × p_config

• p_local is the probability of a suitable collection of proteins being drawn from a set of existing proteins which includes the ones required. Dembski assumes that the proteins are randomly drawn from among the 4289 proteins coded for by E. coli's DNA, that 5 copies are needed of each of 50 different proteins (making 250 proteins altogether), and that, in each case, there are 10 different proteins that would be acceptable (i.e. there are 9 possible substitutes for the real protein. In effect, we have to make 250 draws, and at each draw we have a 500/4289 probability of picking a useful protein, giving an overall probability of (500/4289)²⁵⁰.

• p_config is the probability that, given the right collection of proteins, they will form a viable flagellum if arranged at random. Dembski aims to draw from a uniform probability distribution over all the possible ways of arranging the selected proteins:

  Strictly speaking, the configuration probability for a discrete combinatorial object that exhibits some function is the ratio of all the ways of arranging its building blocks that preserve the function divided by all the possible ways whatsoever of arranging the building blocks. [pp. 294-295]

  Since he can't calculate this directly, he uses an approximation that he calls a perturbation probability. We need not concern ourselves with the details.

• p_orig is the probability of all the individual proteins forming by random combination of amino acids, and is again based on a perturbation probability.

Each of these probabilities individually is below Dembski's universal probability bound, so he does not proceed to multiply them.

Incidentally, Dembski errs in choosing to calculate a formation probability for the flagellum itself. He should have considered the formation of the DNA to code for a flagellum. If a flagellum appeared without the DNA to code for it, it would not be inherited by the next generation of bacteria, and so would be lost.

4.2 Irreducible Complexity

In order to justify his failure to calculate the probability of the flagellum arising by Darwinian evolution, Dembski invokes the notion of irreducible complexity, which, he argues, provides a proscriptive generalization against Darwinian evolution of the flagellum. Irreducible complexity was introduced into the Intelligent Design argument by biochemist Michael Behe. The subject has been addressed in great detail elsewhere, so I will not repeat all the objections.¹⁵ However, I would like to draw attention to a point which some readers of Behe have overlooked. Behe divided potential Darwinian pathways for the evolution of an irreducibly complex (hereafter IC) system into two categories: direct and indirect.¹⁶ The direct pathways are those in which a system evolves purely by the addition of several new parts that provide no advantage to the system until all are in place. All other potential pathways are referred to as indirect. Behe then argues that IC systems cannot evolve via direct pathways. But his direct pathways exclude two vital elements of the evolutionary process: (a) the evolution of individual parts of a system; and (b) the changing of a system's function over time, so that, even though a given part may have contributed nothing to the system's current function until the other parts were in place, it may well have contributed to a previous function. When it comes to indirect pathways, Behe has nothing but an argument from ignorance: no one has given a detailed account of such a pathway. The truth of this assertion has been contested, but it depends on just how much detail is demanded. Behe demands a great deal. He then asserts that the evolution of an IC system by indirect pathways is extremely improbable, but he has provided no argument to support this claim. It is merely his intuition.¹⁷

Dembski repeats the claim that the problem of explaining the evolution of IC molecular systems has "proven utterly intractable" (p. 246), but evolutionary explanations have now been proposed for several of the systems cited by Behe, including the blood-clotting cascade, the immune system, the complement system and the bacterial flagellum. The last of these is highly speculative, but is sufficient to refute the claim of utter intractability.¹⁸

What then has Dembski added to the debate over irreducible complexity? First, he has attempted to counter the objections of Behe's critics. I won't comment on these except to say that some of these critics appear to have misunderstood what Behe meant by irreducible complexity. This is unsurprising since his definition was vague and was accompanied by several misleading statements. Indeed, Behe himself has admitted that his definition was ambiguous.¹⁹ He has even tentatively proposed a completely new definition.²⁰

Second, Dembski has proposed a new definition of his own, making three major changes:

• Behe was very vague about how a system should be divided into parts. Sometimes he took individual proteins as his parts, but in the case of the bacterial flagellum he divided the system into just three parts, "a paddle, a rotor, and a motor", each consisting of multiple proteins (Darwin's Black Box, p. 72). Dembski requires the parts to be "nonarbitrarily individuated" (p. 285), which doesn't tell us much. What is significant, however, is that in the case of the bacterial flagellum he chooses individual proteins as his parts. In fact, he seems not to have even noticed that Behe divided the flagellum into only three parts:

  Behe shows that the intricate machinery in this molecular motor--including a rotor, a stator, O-rings, bushings, and a drive shaft--requires the coordinated interaction of about thirty proteins and another twenty or so proteins to assist in their assembly. Yet the absence of any one of these proteins would result in the complete loss of motor function.... But a flagellum without its full complement of protein parts does not function at all. Behe therefore concludes that if the Darwinian mechanism is going to produce the flagellum, it will have to do so in one generation. [pp. 249-251]

• Whereas Behe only considered a system to be IC if all of its parts were indispensable, Dembski considers a system IC if it has an irreducible core of indispensable parts.

• Dembski has added two new conditions which must be met before a system can be considered evidence of intelligent design. In addition to being IC, the system's irreducible core must possess "numerous and diverse parts" and have the property of "minimal complexity and function" (p. 287). Both of these conditions are rather vague. "Numerous" and "diverse" are not quantified. The complexity of the system apparently need not be quite minimal, since, in the case of the bacterial flagellum, Dembski argues only that "the complexity of known flagella is not very different from the minimal complexity that such systems might in principle require" (p. 288, my emphasis).

The last of these changes is sure to create yet more confusion. It is no longer enough, according to Dembski, to show that a system is IC. It must also meet the two additional criteria. Yet, elsewhere in his book, Dembski continues to refer to irreducible complexity as a sufficient condition for inferring design:

In particular, the claim that the Darwinian mechanism can account for the full diversity of living forms will have to be rejected inasmuch as this mechanism is unable to generate the specified complexity inherent in--to take the most popular example--irreducibly complex biochemical systems (see chapter 5). [p. 324]

I can understand the temptation to use irreducibly complex as a shorthand term for irreducibly complex with an irreducible core which has numerous and diverse parts and exhibits minimal complexity and function, but Dembski should really have introduced a new term for the latter. From now on, when claiming to have found an example of irreducible complexity in nature, Intelligent Design proponents should specify which of the following definitions they have in mind: Behe's original definition; Behe's corrected version of his original definition; Behe's proposed new definition; Dembski's definition; or Dembski's definition plus the two additional criteria. I predict most will fail to do so. For the remainder of this article, I will use the term IC in the last of these senses. It should not be assumed that all the examples of IC systems offered by Behe necessarily meet Dembski's criteria. Dembski considers only the bacterial flagellum. Whether Behe's other example systems are IC in this new sense remains to be established.

Let us accept, for the sake of argument, that Dembski's definition is tight enough to ensure that IC systems cannot evolve by direct pathways. What has he said on the vital subject that Behe failed to address--the subject of indirect pathways? The answer is nothing. The crux of his argument is this:

To achieve an irreducibly complex system, the Darwinian mechanism has but two options. First, it can try to achieve the system in one fell swoop. But if an irreducibly complex system's core consists of numerous and diverse parts, that option is decisively precluded. The only other option for the Darwinian mechanism then is to try to achieve the system gradually by exploiting functional intermediates. But this option can only work so long as the system admits substantial simplifications. The second condition [that the irreducible core of the system is at the minimal level of complexity needed to perform its function] blocks this other option. Let me stress that there is no false dilemma here--it is not as though there are other options that I have conveniently ignored but that the Darwinian mechanism has at its disposal.[p. 287]

But there is indeed an option that Dembski has overlooked. The system could have evolved from a simpler system with a different function. In that case there could be functional intermediates after all. Dembski's mistake is to assume that the only possible functional intermediates are intermediates having the same function.

Dembski's failure to consider the possibility of a change of function is seen in his definition of irreducible complexity:

Definition IC_final--A system performing a given basic function is irreducibly complex if it includes a set of well-matched, mutually interacting, non-arbitrarily individuated parts such that each part in the set is indispensable to maintaining the system's basic, and therefore original, function. The set of these indispensable parts is known as the irreducible core of the system. [p. 285]

There is no reason why a system's basic function should be its original one. The concepts of basic function and original function may not even be well-defined. If a system performs two vital functions, which is the basic one? The concept of an original function assumes there is an identifiable time at which the system came into existence. But the system may have a long history in which parts have come and gone, and functions have changed, making it impossible to trace back the origin of the system to one particular time. And what is a system? If two proteins start to interact in a beneficial way , do they immediately become a system? If so, we may have to trace the history of a system all the way back to the time when one it was just two interacting proteins.

There is a tendency among antievolutionists to think of biological systems as if they were like man-made machines, in which the system and its parts have been designed for one specific function and are difficult to modify for another function. But biological systems are much more flexible and dynamic than man-made ones.

A few other points are worth noting:

• Changes of function are not an ad hoc idea thought up as a last-ditch attempt to solve a nasty problem. They are a fundamental feature of evolution. New systems do not just appear out of nowhere. Most systems will have evolved from an earlier system having a different function.

• Changes of function can occur in two ways. First, a mutation may create a new capability. Second, a change in the environment may provide a new use for a system, e.g. a fish's fin starts to be used as a primitive leg in shallow water. In either case, the system may perform the new function very poorly at first, subsequently mutating to perform it better. Behe and Dembski both emphasize how well coordinated the parts of a system seem to be. But they may have been far less well coordinated in the past.

• A system may have more than one function. In the example above, the fish's fin may continue to be used for swimming as well as clambering over submerged rocks.

• There is no clear distinction between systems and parts. Any functional structure can be considered both a system in its own right and a part of a larger system. So we need not think in terms of a system acquiring a large number of parts consisting of individual proteins, as Dembski would have us do. A system may instead acquire a small number of sub-systems, each consisting of multiple proteins.

• Instead of an IC system having to arise by the simultaneous combination of many parts, we now see that it can arise by the gradual acquisition of a few parts. This no longer sounds as unlikely as Behe and Dembski made it seem.

Before finishing this section, it might be useful to clear up a few more red herrings which Dembski introduces into his discussion of irreducible complexity.

• Causal specificity. This is just another cover for the argument from ignorance:

  Unless a concrete model is put forward that is detailed enough to be seriously criticized, then it is not going to be possible to determine the adequacy of that model. This is of course another way of saying that the scaffolding objection has yet to demonstrate causal specificity when applied to actual irreducibly complex biochemical systems. [p. 254]

  In other words, until a sufficiently detailed natural hypothesis is provided, we should go ahead and infer design. It doesn't bother Dembski (or Behe who makes the same point) that their alternative hypothesis (design) lacks any details whatsoever.

• Invariants. Dembski describes some geometrical problems which have no solution, and explains how the non-existence of a solution can be proven by showing that a certain property is invariant under transformation of the system. How is this relevant to irreducible complexity? Does Dembski use the invariance of some property to establish that IC systems cannot evolve? No, the property he claims to be invariant (under natural evolution) is the property of irreducible complexity itself. But the assertion that irreducible complexity cannot be produced by natural evolution was exactly the point which he was trying to establish. In other words, invariance does no work in establishing Dembski's conclusion. It is just another way of expressing that conclusion.

  In trying to relate the subject of invariants to evolution, Dembski writes: "think of an effective invariant here as an insurmountable obstacle for the Darwinian mechanism" (p. 285). One has to wonder why he does not just use the expression "insurmountable obstacle" from the start, and skip the whole irrelevant discussion of invariants.

• Specified complexity. Dembski likes to say that "irreducible complexity is a special case of specified complexity" (p. 289), as if this demonstrated the integration of two concepts into a coherent framework. But we have already seen that specified complexity is merely a label we apply when we have no plausible natural hypothesis to explain some event. So, to say that irreducible complexity is a case of specified complexity is just another way to repeat the claim that we have no natural explanation for the origin of the bacterial flagellum (which is the only biological system Dembski has shown to be IC in his sense).

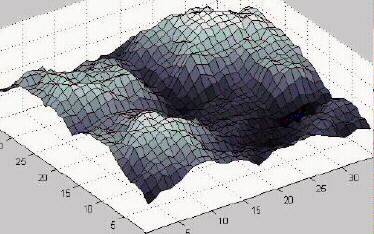
5. Evolutionary Algorithms

Attempt the end, and never stand to doubt;
Nothing's so hard, but search will find it out.
Robert Herrick (1591-1674)

In recent years there has been a considerable growth of interest in evolutionary algorithms, executed on computers, as a means for solving optimization problems. As the name suggests, evolutionary algorithms are based on the same underlying principles as biological evolution: reproduction with random variations, and selection of the "fittest". Since they appear to demonstrate how unguided processes can produce the sort of functional complexity²¹ that we see in biology, they are a problem which Dembski needs to address. In addition, he tries to turn the subject to his advantage, by appealing to a set of mathematical theorems, known as the No Free Lunch theorems, which place constraints on the problem-solving abilities of evolutionary algorithms.

5.1 Black-Box Optimization Algorithms

We will be concerned here with a type of algorithm know as a black-box optimization (or search) algorithm. Such algorithms include evolutionary algorithms, but are not limited to them. The problems which black-box optimization algorithms solve have just two defining attributes: a phase space, and a fitness function defined over that phase space. In the context of these algorithms, phase spaces are usually called search spaces. Also the term fitness function is usually reserved for evolutionary algorithms, the more general term being objective function or cost function (maximizing an objective function is equivalent to minimizing a cost function). But I will adopt Dembski's terminology for the sake of consistency.

The phase space is the set of all potential solutions to the problem. It is generally a multidimensional space, with one dimension for each variable parameter in the solution. Most real optimization problems have many parameters, but, for ease of understanding, it is helpful to think of a two-dimensional phase space--one with two parameters--which can be visualized as a horizontal plane. The fitness function is a function over this phase space; in other words, for every point (potential solution) in the phase space the fitness function tells us the fitness value of that point. We can visualize the fitness function as a three-dimensional landscape where the height of a point represents its fitness (figure 1). Points on hills represent better solutions while points in valleys represent poorer ones. The terms fitness function and fitness landscape are used interchangeably.

Figure 1. A Fitness Landscape

An optimization algorithm is, broadly speaking, an algorithm for finding high points in the landscape. Being a black-box algorithm means that it has no knowledge about the problem it is trying to solve other than the underlying structure of the phase space and the values of the fitness function at the points it has already visited. The algorithm visits a sequence of points (x₁, x₂, ..., x_m), evaluating the fitness, f(x_i), of each one in turn before deciding which point to visit next. The algorithm may be stochastic, i.e. it may incorporate a random element in its decisions.

Evaluating the fitness function is typically a very computation-intensive process, possibly involving a simulation. For example, if we are trying to optimize the design of a road network, we might want the algorithm to run a simulation of daily traffic for each possible design that it considers. The performance of the algorithm is therefore measured in terms of the number of fitness function evaluations (m) needed to reach a given level of fitness, or the level of fitness reached after a given number of function evaluations. Each function evaluation can be thought of as a time step, so we can think in terms of the level of fitness reached in a given time. Note that we are interested in the best fitness value found throughout the whole time period, and not just the fitness of the last point visited.

There are three types of optimization algorithm of interest to us here:

• Random search (also known as random sampling). This algorithm just selects each point at random (with a uniform probability distribution) out of all the points in the phase space.

• Hill-climbers. A hill-climber visits some or all the points near to its current location, and moves to the highest one it finds. It never moves downwards. If it reaches the top of a hill, it gets stuck there, or it may begin a random search in the hope of finding a higher hill.

• Evolutionary algorithms. An evolutionary algorithm maintains a population of individuals (usually randomly generated initially), that evolves according to rules of selection, recombination, mutation and survival. Each individual corresponds to a point in the phase space. A shared "environment" determines the fitness of each individual in the population. The fittest individuals are more likely to be selected for reproduction (retention or duplication), while recombination and mutation modify those individuals, yielding potentially superior ones.

Dembski adopts a very broad definition of evolutionary algorithm which includes all the optimization algorithms which we consider here, including random search (pp. 180, 229n9, 232n31).

Another term used by Dembski is blind search. He uses it in two senses. First it means a random walk, an algorithm which moves from one location in the phase space to another location selected randomly from nearby points (p. 190). Later he uses it to mean any search in which the fitness function has only two possible values: the point being evaluated either is or is not in a target area (p. 197). The usual (though not exclusive) meaning of blind search in the literature of evolutionary algorithms is as a synonym for black-box algorithm.²²

5.2 Fine-Tuning the Fitness Function

Dembski recognizes that evolutionary algorithms can produce quite innovative results, but he argues that they can only do so because their fitness function has been fine-tuned by the programmer. In doing so, he alleges, the programmer has "smuggled" complex specified information or specified complexity into the result. (These two terms will be discussed later.)

Even so, there is something oddly compelling and almost magical about the way evolutionary algorithms find solutions to problems where the solutions are not like anything we have imagined. A particularly striking example is the "crooked wire genetic antennas" of Edward Altshuler and Derek Linden. The problem these researchers solved with evolutionary (or genetic) algorithms was to find an antenna that radiates equally well in all directions over a hemisphere situated above a ground plane of infinite extent. Contrary to expectations, no wire with a neat symmetric geometric shape solves this problem. Instead, the best solutions to this problem look like zigzagging tangles. What's more, evolutionary algorithms find their way through all the various zigzagging tangles--most of which don't work--to one that actually does. This is remarkable. Even so, the fitness function that prescribes optimal antenna performance is well-defined and readily supplies the complex specified information that an optimal crooked wire genetic antenna seems to acquire for free. [p. 221]

A similar claim is made regarding biological evolution:

Thus I submit that even if Darwinian evolution is the means by which the panoply of life on earth came to be, the underlying fitness function that constrains biological evolution would not be a free lunch and not a brute given, but a finely crafted assemblage of smooth gradients that presupposes much prior specified complexity. [p. 212]

These claims are based on a fundamental misconception of the role of the fitness function in an evolutionary algorithm. A fitness function incorporates two elements:

• It reflects our objectives. If our aim is to design a bridge, we might need to decide what weight to give to a number of conflicting objectives such as traffic capacity, structural integrity, cost and environmental impact.

• It encapsulates our relevant knowledge about the real world, in order to evaluate how well a potential solution meets our objectives.

In general, then, the fitness function defines the problem to be solved, not the way to solve it, and it therefore makes little sense to talk about the programmer fine-tuning the fitness function in order to solve the problem. True, there may be some aspects of the problem which are unknown, or where the programmer decides, for practical reasons, to simplify his model of the problem. Here the programmer could make decisions in such a way as to improve the performance of the algorithm. But there is no reason to think that this makes a significant contribution to the success of evolutionary algorithms.

In one of his articles, Dembski quotes evolutionary psychologist Geoffrey Miller in support of his claim that the fitness function needs to be fine-tuned:

And where exactly does design get built into an evolutionary or genetic algorithm? According to Miller, it gets built into the fitness function. He writes:

The fitness function must embody not only the engineer's conscious goals, but also her common sense. This common sense is largely intuitive and unconscious, so is hard to formalize into an explicit fitness function. Since genetic algorithm solutions are only as good as the fitness functions used to evolve them, careful development of appropriate fitness functions embodying all relevant design constraints, trade-offs and criteria is a key step in evolutionary engineering.²³

But the engineer's goals, constraints, trade-offs, etc, are parameters of the problem to be solved. They must be carefully chosen to ensure that the evolutionary algorithm addresses the right problem, not to guide it to the solution of a given problem, as Miller tells us in the preceding paragraph:

If the fitness function does not realistically reflect the real-world constraints and demands that the phenotypic designs will face, the genetic algorithm may deliver a good solution to the wrong problem.²⁴

It is other elements of the evolutionary algorithm which may have to be carefully selected if the algorithm is to perform well:

The trick in genetic algorithms is to find schemes that do this mapping from a binary bit-string to an engineering design efficiently and elegantly, rather than by brute-force.... The genetic operators copy and modify the genotypes from one generation to the next.... Getting the right balance between mutation and selection is especially important.... Finally, the evolutionary parameters [such as population size and mutation rate] determine the general context for evolution and the quantitative details of how the genetic operators work.... Deciding the best values for these parameters in a given application remains a black art, driven more by blind intuition and communal tradition than by sound engineering principles.²⁴

A similar point is made by Wolpert and Macready:

Ultimately, of course, the only important question is, "How do I find good solutions for my given cost function f?" The proper answer to this question is to start with the given f, determine certain salient features of it, and then construct a search algorithm, a, specifically tailored to match those features. The inverse procedure--far more popular in some communities--is to investigate how specific algorithms perform on different f's. This inverse procedure is only of interest to the degree that it helps us with our primary procedure, of going from (features concerning) f to an appropriate a.²⁵

Perhaps Dembski's confusion on this subject can be explained by his obsession with Richard Dawkins' Weasel program,²⁶ to which he devotes a large part of his chapter on evolutionary algorithms. In that example, invented only to illustrate one specific point, the fitness function was indeed chosen in order to help the algorithm converge on the solution. That program, however, was not created to solve an optimization problem. The program had a specific target point, unlike real optimization algorithms, where the solution is unknown.

In the case of biological evolution, the situation is somewhat different, because the evolutionary parameters themselves evolve over the course of evolution. For example, according to evolutionary theory, the genetic code has evolved by natural selection. It is therefore not just good luck that the genetic code is so suited to evolution. It has evolved to be that way.

When Dembski talks about fine-tuning of the fitness function for biological evolution, what he really means is fine-tuning of the cosmological and terrestrial initial conditions, including the laws of physics. When these conditions are a given, as they are for practical purposes, they contribute to determining the fitness function. But Dembski argues that these conditions must have been selected from a set of alternative possibilities in order to make the evolution of life possible. When considered in this way, alternative sets of initial conditions should properly be considered as elements in another phase space, and not as part of the fitness function. Dembski sometimes refers to this as a phase space of fitness functions. One can understand what he means by this, but it is potentially confusing, not least because the fitness functions for biological organisms are not fixed, but evolve as their environment evolves.

We see then that Dembski's argument from fine-tuning of fitness functions is just a disguised version of the well-known argument from fine-tuning of cosmological and terrestrial initial conditions.²⁷ Dembski lists a catalogue of cosmological and terrestrial conditions which need to be just right for the origin of life (pp. 210-211). This argument is an old one, and I won't address it here. The only new twist that Dembski gives to it is to cast the argument in terms of fitness functions and appeal to the No Free Lunch theorems for support. That appeal will be considered below, but first I want to make a couple of observations.

Dembski's two conclusions cannot both be true. On the one hand he is arguing that the initial conditions were fine-tuned to make natural evolution of life possible. On the other hand, he is arguing that natural evolution of life wasn't possible. Not that there's anything wrong with Dembski having two bites at the cherry. If one argument fails, he can fall back on the other. Alternatively Dembski might argue that the cosmic designer made the Universe almost right for the natural evolution of life, but left himself with a little work to do later.

If Dembski believes that the initial conditions for evolution were designed, the obvious thing to do would be to try applying his chance-elimination method to the origin of those conditions. I note that he doesn't attempt to do so.

5.3 The No Free Lunch Theorems

Dembski attempts to use the No Free Lunch theorems (hereafter NFL) of David Wolpert and William Macready²⁸ to support his claim that fitness functions need to be fine-tuned. He presumably considers NFL important to his case, since he names his book after it. However, I will show that NFL is not applicable to biological evolution, and even for those evolutionary algorithms to which it does apply, it does not support the fine-tuning claim. I'll start by giving a brief explanation of what NFL says, making a number of simplifications and omitting details which need not concern us here.

NFL applies only to algorithms meeting the following conditions:

• The algorithm must be a black-box algorithm, i.e. it has no knowledge about the problem it is trying to solve other than the underlying structure of the phase space and the values of the fitness function at the points it has already visited.

• In principle, there must be a finite number of points in the phase space and a finite number of possible fitness values. In practice, however, continuous variables can be approximated by rounding to discrete values.

• The algorithm must not visit the same point twice. This can be avoided by having the algorithm keep a record of all the points it has visited so far, with their fitness values, so it can avoid repeated visits to a point. This may not be practical in a real computer program, but most real phase spaces are sufficiently vast that revisits are unlikely to occur often, so we can ignore this issue.

• The fitness function may remain fixed throughout the execution of the program, or it may vary over time in a manner which is independent of the progress of the algorithm. These two options correspond to Wolpert and Macready's Theorems 1 and 2 respectively. However, the fitness function may not vary in response to the progress of the algorithm. In other words, the algorithm may not deform the fitness landscape.²⁹

The same algorithm can be used with any problem, i.e. on any fitness landscape, though it won't be efficient on all of them. In terms of a computer program, we can imagine inserting various alternative fitness function modules into the program. We can also imagine the set of all possible fitness functions. This is the vast set consisting of every possible shape of landscape over our given phase space. If there are S points in the phase space and F possible values of the fitness function, then the total number of possible fitness functions is F^S, since each point can have any of F values, and we must allow for every possible permutation over the S points.

We are now in a position to understand what NFL says. Suppose we take an algorithm a₁, measure its performance on every fitness function in that vast set of possible fitness functions, and take the average over all those performance values. Then we repeat this for any other algorithm a₂. NFL tells us that the average performance will be the same for both algorithms, regardless of which pair of algorithms we selected. Since it is true for all pairs of algorithms, and since random search is one of these algorithms, this means that no algorithm is any better (or worse) than a random search, when averaged over all possible fitness functions. It even means that, averaged over all possible fitness functions, a hill-descending algorithm will be just as good as a hill-climbing algorithm at finding high points! (A hill-descender is like a hill-climber except that it moves to the lowest of the available points instead of the highest.)

This result seems incredible, but it really is true. The important thing to remember is the vital phrase "averaged over the set of all possible fitness functions". The vast majority of fitness functions in that set are totally chaotic, with the height of any two adjacent points being unrelated. Only a minuscule number of those fitness functions have the smooth rolling hills and valleys that we usually associate with a "landscape". In a chaotic landscape, there are no hills worthy of the name to be climbed. Furthermore, remember that every point which a hill-climber or descender peeks at counts as having been "found", even if the algorithm decides not to move there. So if a hill-descender happens to move adjacent to a very tall spike, the fitness value at that spike will be recorded and will count in the descender's final performance evaluation. A landscape picked at random from the set of all possible fitness functions will almost certainly be just a random mass of spikes (figure 2).

Figure 2. A Random Fitness "Landscape"

We can already see that the relevance of NFL to real problems is limited. The fitness landscapes of real problems are not this chaotic. This fact has been noted by a number of researchers:

In spite of the correctness of this "no-free-lunch theorem" (Wolpert and Macready 1997) the result is not too interesting. It is easy to see, that averaging over all different fitness functions does not match the situation of black-box optimization in practice. It can even be shown that in more realistic optimization scenarios there can be no such thing as a no-free-lunch theorem (Droste, Jansen, and Wegener 1999).³⁰

5.4 The Irrelevance of NFL to Dembski's Arguments

NFL is not applicable to biological evolution, because biological evolution cannot be represented by any algorithm which satisfies the conditions given above. Unlike simpler evolutionary algorithms, where reproductive success is determined by a comparison of the innate fitness of different individuals, reproductive success in nature is determined by all the contingent events occurring in the lives of the individuals. The fitness function cannot take these events into account, because they depend on interactions with the rest of the population and therefore on the characteristics of other organisms which are also changing under the influence of the algorithm. In other words, the fitness function of biological organisms changes over time in response to changes in the population (of the same species and of other species), violating the final condition listed above. The same also applies to any non-biological simulations in which the individuals interact with each other, such as the competing checkers-playing neural nets which are discussed below.

It would do no good to suggest that the interactions between individuals could be modelled within the optimization algorithm, rather than in the fitness function. This is prevented by the black-box constraint, which stops the optimization algorithm having direct access to information about the environment.

This is similar to the problem of coevolving fitness landscapes raised by Stuart Kauffman (p. 224-227). Dembski's response to Kauffman, however, does not address my argument. Nothing that Dembski writes (p. 226) changes the fact that, in biological evolution, the fitness function at a given time cannot be determined independently of the state of the population, and therefore NFL does not apply.³¹

Moreover, NFL is hardly relevant to Dembski's argument even for the simpler, non-interactive evolutionary algorithms to which it does apply (those where the reproductive success of individuals is determined by a comparison of their innate fitness). NFL tells us that, out of the set of all mathematically possible fitness functions, there is only a tiny proportion on which evolutionary algorithms perform as well as they are observed to do in practice. From this, Dembski argues that it would be incredibly fortuitous for a suitable fitness function to occur without fine-tuning by a designer. But the alternative to design is not purely random selection from the set of all mathematically possible fitness functions. Fitness functions are determined by rules, not generated randomly. In the real world, these rules are the physical laws of the Universe. In a computer model, they can be whatever rules the programmer chooses, but, if the model is a simulation of reality, they will be based to some degree on real physical laws. Rules inevitably give rise to patterns, so that patterned fitness functions will be favoured over totally chaotic ones. If the rules are reasonably regular, we would expect the fitness landscape to be reasonably smooth. In fact, physical laws generally are regular, in the sense that they correspond to continuous mathematical functions, like "F = ma", "E = mc²", etc. With these functions, a small change of input leads to a small change of output. So, when fitness is determined by a combination of such laws, it's reasonable to expect that a small movement in the phase space will generally lead to a reasonably small change in the fitness value, i.e. that the fitness landscape will be smooth. On the other hand, we expect there to be exceptions, because chaos theory and catastrophe theory tell us that even smooth laws can give rise to discontinuities. But real phase spaces have many dimensions. If movement in some dimensions is blocked by discontinuities, there may still be smooth contours in other dimensions. While many potential mutations are catastrophic, many others are not.

Dembski might then argue that this only displaces the problem, and that we are incredibly lucky that the Universe has regular laws. Certainly, there would be no life if the Universe did not have reasonably regular laws. But this is obvious, and is not specifically a consequence of NFL. This argument reduces to just a variant of the cosmological fine-tuning argument, and a particularly weak one at that, since the "choice" to have regular laws rather than chaotic ones is hardly a very "fine" one.

Although it undermines Dembski's argument from NFL, the regularity of laws is not sufficient to ensure that real-world evolution will produce functional complexity. Dembski gives one laboratory example where replicating molecules became simpler (the Spiegelman experiment, p. 209). But it does not follow that this is always so. Dembski has not established any general rule. I would suggest that, because the phase space of biological evolution is so massively multidimensional, we should not be surprised that it has produced enormous functional complexity.

6. The Uniform-Probability Method

Operator... Give me Information.
Song by William Spivery

6.1 Derived Design

Dembski tells us that he has two different arguments for design in nature. As well as attempting to show that there exist in nature phenomena which Darwinian evolution does not have the ability to generate (such as the bacterial flagellum), Dembski also deploys another argument. Even if Darwinian evolution did have that ability, he argues, it could only have it by virtue of there having been design involved in the selection of the initial conditions underlying evolution.

The Darwinist therefore objects that "real life" Darwinian evolution can in fact generate specified complexity without smuggling it in after all. The fitness function in biological evolution follows directly from differential survival and reproduction, and this, according to the Darwinist, can legitimately be viewed as a "free lunch".... If this objection is conceded, then the only way to show that the Darwinian mechanism cannot generate specified complexity is by demonstrating that the gradients of the fitness function induced by differential survival and reproduction are not sufficiently smooth for the Darwinian mechanism to drive large-scale biological evolution. To use another Dawkins metaphor, one must show that there is no gradual way to ascend "Mount Improbable." This is a separate line of argument and one that I shall take up in the next chapter [which addresses irreducible complexity and the bacterial flagellum]. Here, however, I want to show that this concession need not be granted and that the displacement problem does indeed undercut Darwinism. [p. 208]

This is an argument for what I will call derived design. (Dembski uses the term derived intentionality.) It does not argue for design in a particular event (such as evolution of some structure), but merely argues that design must have been involved at some point or other in the causal chain of events leading to some phenomenon that we observe.

We have already seen this argument cast in terms of fine-tuning of fitness functions. Dembski also casts it in terms of specified complexity. Earlier, specified complexity was introduced as something to be inferred when we had eliminated all the natural hypotheses we could think of to explain an event. But now Dembski is telling us that, even if we cannot eliminate Darwinian evolution as an explanation, we should still make an inference of derived design if we observe specified complexity. Clearly, then, this is a different meaning of specified complexity. This new meaning is an observed property of a phenomenon, not an inferred property of an event. It indicates that the phenomenon has a complex (in a special sense) configuration. This property also goes by the name of complex specified information (CSI).

Note that this is another purely eliminative method; it infers design from the claimed absence of any natural process capable of generating CSI. If the claim were true, it could be considered a proscriptive generalization, but we will see that the claim has no basis whatsoever.

6.2 Complex Specified Information (CSI)

Dembski devises his own measure of how complex a phenomenon's configuration is, and calls it specified information (which I'll abbreviate to SI). He calculates this measure by choosing a specification (as described in 3.1 above) and then calculating the probability of an outcome matching that specification as if the phenomenon was generated by a process having a uniform probability distribution. A uniform probability distribution is one in which all possible outcomes (i.e. configurations) have the same probability, and Dembski calculates the SI on this basis even if the phenomenon in question is known not to have been generated by such a process. (This will be considered more carefully in the next section.) The probability calculated in this way is then converted into "information" by applying the function I(R) = -log₂P(R), i.e. the information is the negation of the logarithm (base 2) of the probability, and he refers to the resulting measure as a number of bits.

If the SI of a phenomenon exceeds a universal complexity bound of 500 bits, then Dembski says that the phenomenon exhibits complex specified information (or CSI).³² The universal complexity bound is obtained directly from Dembski's universal probability bound of 10^-150, since -log₂(10^-150) is approximately 500. Dembski also refers to CSI as specified complexity, using the two terms interchangeably. As noted above, this meaning of specified complexity is different from the one we encountered earlier. I'll call it uniform-probability specified complexity. To be clear: eliminative specified complexity is an inferred attribute of an event, indicating that we believe the event was highly improbable with respect to all known causal mechanisms; uniform-probability specified complexity (or CSI) is an observed attribute of a phenomenon, indicating that the phenomenon has a "complex" configuration, without regard to how it came into existence. We will see that Dembski's notion of "complexity" is very different from our normal understanding of the word.

6.3 Evidence For The Uniform-Probability Interpretation

The fact that the probability used to calculate SI is always based on a uniform probability distribution is extremely important. Dembski uses a uniform (or "purely random") distribution even if the phenomenon is known to have been caused by a process having some other probability distribution. Since this is not explicitly stated by Dembski, and may seem surprising, I will present several items of evidence to justify my interpretation.

Exhibit #1 -- The derived design argument

As argued in 6.1 above, Dembski's derived design argument implies that SI is an observed property of a phenomenon, which allegedly allows us to infer design in the distant past regardless of what subsequent natural processes might have led to the phenomenon. There are therefore no relevant probability distributions under which to calculate the probability for SI. We must use some default probability distribution, and a uniform distribution seems to be the only candidate.

Exhibit #2 -- The Weasel program²⁶

Here Dembski specifically mentions a uniform probability distribution:

For instance, in Dawkins's METHINKS-IT-IS-LIKE-A-WEASEL example (see section 4.1), the phase space consists of all sequences 28 characters in length comprising upper case Roman letters and spaces (spaces being represented by bullets). A uniform probability on this space assigns equal probability to each of these sequences--the probability value is approximately 1 in 10⁴⁰ and signals a highly improbable state of affairs. It is this improbability that corresponds to the complexity of the target sequence and which by its explicit identification specifies the sequence and thus renders it an instance of specified complexity (though as pointed out in section 4.1, we are being somewhat loose in this example about the level of complexity required for specified complexity--technically, the level of complexity should correspond to the universal probability bound of 1 in 10¹⁵⁰). [p. 188-189]

This seems clear. However, Dembski goes on to say that "E [the evolutionary algorithm] has in fact not generated specified complexity at all but merely shifted it around" (p. 195). (By this point Dembski has switched to another version of the Weasel program, but the change is inconsequential.) Although he fails to state it explicitly, the implication is that the outcome does exhibit specified complexity, though this was "smuggled" into the program and not generated by it.

Exhibit #3 -- Evolutionary algorithms

My next piece of evidence comes from Dembski's accounts of Tom Schneider's binding site simulation³³ (pp. 213-218) and the checkers-playing neural nets of Kumar Chellapilla and David Fogel (pp. 221-223), which I will describe later. These programs have a high probability of producing a good solution (as has been confirmed to me by their programmers). Since Dembski asserts that the outcomes exhibited specified complexity (CSI), which implies a low probability of producing a specified result (a good solution), it follows that he must have been estimating the probability with respect to some probability distribution other than the true one. The only apparent candidate is a uniform probability distribution.

Exhibit #4 -- The SETI sequence

One of Dembski's examples (pp. 6-9) is an event from the film Contact, starring Jodie Foster, in which astronomers at SETI (the Search for Extraterrestrial Intelligence) detect a radio signal of extraterrestrial origin. The signal comprises a sequence of 1126 beats and pauses, representing the first 25 prime numbers: 2, 3, 5, 7, ..., 101. Each prime number is represented by a sequence of beats equal to the number, with consecutive numbers separated by a pause. Converting the beats to 1s and the pauses to 0s, the signal can be represented by a sequence of 1126 binary digits (bits), beginning "110111011111011111110...". The fictional astronomers immediately recognized this signal as having an intelligent origin.

Dembski tells us that the SETI sequence exhibits specified complexity (p. 359). On pp. 143-144 he gives an abbreviated 1000-bit version of this sequence, telling us that it has a probability of 1 in 2¹⁰⁰⁰, giving SI of over 500 bits (presumably 1000 bits). The latter example is based on a known cause (intelligent agency or coin tossing), but presumably the sequence has the same SI regardless of its cause. After all, we don't know the true cause of the SETI sequence, yet Dembski still tells us it exhibits specified complexity. It is very unlikely that the SETI sequence was produced by the equivalent of coin tossing. A much more likely scenario is that the extraterrestrials have programmed a computer to generate the sequence automatically. In that case, we're back to the same sort of situation as the Weasel program. Furthermore, if we were considering all relevant chance hypotheses, we should consider the possibility that the two alternative outcomes of each beat/pause were not equally likely. In the absence of any other information, the best estimate of the probabilities of beat and pause would be 1102/1126 and 24/1126 respectively, since we observed 1102 beats and 24 pauses. With these probabilities (and still assuming that each beat/pause is independent of the others), the probability of receiving the SETI sequence would be (1102/1126)¹¹⁰² × (24/1126)²⁴ = 3.78 × 10^-51, considerably larger than the universal probability bound of 10^-150. I therefore conclude that Dembski calculates the SI of the SETI sequence on the basis of the beats and pauses having equal probability (1/2) and that the sequence exhibits 1126 bits of SI.

Exhibit #5 -- URF13

Finally, I must mention a counterexample to my uniform-probability interpretation. Dembski considers the case of a gene, T-urf13, which occurs in a particular strain of maize (pp. 218-219). This gene codes for a protein product called URF13. In determining whether URF13 exhibits CSI, Dembski starts by calculating a probability of 20⁸³, on the grounds that the minimal functional size of URF13 is 83 amino acids and that there are 20 possible amino acids. So he is assuming that URF13 is drawn from a uniform probability distribution over the space of all possible sequences of 83 amino acids. He then points out that the probability is really higher than this as we must allow for the possibility of other sequences having the same function as URF13, i.e. other sequences matching the same specification. So far, then, this supports the uniform-probability interpretation. Further down the page, however, he argues that the probability on which SI must be based is higher still:

What if any way we sliced it, the improbabilities computed turned out to be less than the universal probability bound? Would that demonstrate that CSI had been naturalistically generated? No. First off, there is no reason to think that non-protein-coding gene segments themselves are truly random--as noted above, T-urf13, which is composed of such segments, is homologous to ribosomal RNA. So it is not as though these segments were produced by sampling an urn filled with loosely mixed nucleic acids. What's more, it is not clear that recombination itself is truly random. [p. 219]

Now Dembski is saying that we shouldn't just calculate SI based on a uniform probability (urn) model, but should take into account the causal processes which we think are operating. But this contradicts the computer examples given above, where we knew the actual causal process (execution of a computer program) and that process gave a specified result with high probability, yet Dembski told us that the result exhibited CSI anyway.

Although the evidence is inconclusive, it seems to predominantly favour the uniform-probability interpretation, and that is the one that I will consider hereafter. But let me briefly look at the alternatives:

• SI is based on the probability with respect to the true causal process responsible for the event. This would make SI useless for the purpose of making inferences about the cause of a phenomenon. We would need to know the cause in order to infer the cause! Furthermore, it would be meaningless to say that a designed phenomenon exhibits CSI, since there is no probability distribution with respect to which we can calculate the SI of a designed phenomenon (as Dembski tells us that design is not a probabilistic process). This interpretation is clearly untenable.

• SI is based on our best understanding of the causal processes which we think might underlie the event which gave rise to the observed phenomenon. But this is just the chance-elimination method again. We calculate the SI under the best chance hypothesis we can think of (the one conferring the highest probability on a detachable rejection region). If the SI under this chance hypothesis is high enough (probability low enough), we reject this chance hypothesis and infer design. By implication, we have already considered and rejected all the inferior chance hypotheses that we could think of (those conferring only lower probabilities on detachable rejection regions). In that case, the assertion that a phenomenon exhibits CSI is merely an assertion that it is improbable under all the chance hypotheses we can think of. In other words, this is the same argument from ignorance which was addressed earlier.

If Dembski insists that he has only one method of design inference and that it's the chance-elimination method, then he needs to explain away the exhibits above and justify his introduction of the terms "complexity" and "information". The chance-elimination method uses a statistical (probabilistic) technique for eliminating hypotheses. This has nothing to do with complexity or information. Transforming probabilities by applying the trivial function I = -log₂P does not magically convert them into complexity or information measures. It only serves to obfuscate the nature of the argument.

My guess is that Dembski has failed to notice that he has two different methods. One reason for his confusion may be that all the chance hypotheses he ever considers in his examples are ones which give rise to a uniform probability distribution, with the sole exception of one trivial case (p. 70).

Dembski also seems to consider uniform probability distributions "privileged" in some sense (p. 50). Referring to the phase space of an optimization algorithm, he writes:

Moreover, such spaces typically come with a uniform probability that is adapted to the topology of the phase space. What this means is that Ω [the phase space] possesses a uniform probability measure U adapted to the metric on Ω so that geometrically congruent pieces of Ω get assigned identical probabilities (see section 2.2). [p. 188]

But a phase space (as the search space of an optimization algorithm) does not come with a probability distribution attached. It is simply a space of possible solutions which we are interested in searching.³⁴

6.4 The Choice of Phase Space

Although basing SI on a uniform probability distribution helps to make it independent of the causal process which produced the phenomenon, it cannot make it completely independent. Given a phase space (or reference class of possibilities, as Dembski calls it), there is only one possible uniform distribution, the one in which all outcomes have equal probability. But how do we choose a phase space? In the case of the SETI sequence it may seem obvious that the relevant phase space is the space of all possible bit sequences of length 1126. But why should we assume that the sequence was drawn from a space of 1126-bit sequences, and not sequences of variable length? Why should we assume that beat and pause were the only two possible values? The supposed extraterrestrials could have chosen to transmit beats of varying amplitudes.

Similar problems arise elsewhere. On p. 166, Dembski calculates the complexity of the word METHINKS as -log₂(1/27⁸) = 38 bits.³⁵ This is based on a phase space of strings of 8 characters where each character has 27 possi