Version 1.0
[Last Modified: April 23, 2002]
Permission is given to copy and print this page for non-profit personal or educational use.
Summary
1. Introduction
2. Design and Nature
3. The Chance-Elimination Method
| 4.1 A Tornado in a Junkyard | 4.2 Irreducible Complexity |
| 5.1 Black-Box Optimization Algorithms | |
| 5.2 Fine-Tuning the Fitness Function | |
| 5.3 The No Free Lunch Theorems | |
| 5.4 The Irrelevance of NFL to Dembski's Arguments |
| 7.1 Outline of a Positive Research Program | |
| 7.2 Testability | |
| 7.3 Unembodied Designers |
Life is like a box of chocolates. You never know what you're
gonna get.
Forrest Gump
The aim of Dr William Dembski's book No Free Lunch is to demonstrate that design (the action of a conscious agent) was involved in the process of biological evolution. The following critique shows that his arguments are deeply flawed and have little to contribute to science or mathematics. To fully address Dembski's arguments has required a lengthy and sometimes technical article, so this summary is provided for the benefit of readers without the time to consider the arguments in full.
Dembski has proposed a method of inference which, he claims, is a rigorous formulation of how we ordinarily recognize design. If we can show that an observed event or object has low probability of occurring under all the non-design hypotheses (explanations) we can think of, Dembski tells us to infer design. This method is purely eliminative--we are to infer design when we have rejected all the other hypotheses we can think of--and is commonly known as an argument from ignorance, or god-of-the-gaps argument.
Because god-of-the-gaps arguments are almost universally recognized by scientists and philosophers of science to be invalid as scientific inferences, Dembski goes to great length to disguise the nature of his method. For example, he inserts a middleman called specified complexity: after rejecting all the non-design hypotheses we can think of, he tells us to infer that the object in question exhibits specified complexity, and then claims that specified complexity is a reliable indicator of design.
The only biological object to which Dembski applies his method is the flagellum of the bacterium E. coli. First, he attempts to show that the flagellum could not have arisen by Darwinian evolution, appealing to a modified version of Michael Behe's argument from irreducible complexity. However Dembski's argument suffers from the same fundamental flaw as Behe's: he fails to allow for changes in the function of a biological system as it evolves.
Since Dembski's method is supposed to be based on probability and he has promised readers of his earlier work a probability calculation, he proceeds to calculate a probability for the origin of the flagellum. But this calculation is based on the assumption that the flagellum arose suddenly, as an utterly random combination of proteins. The calculation is elaborate but totally irrelevant, since no evolutionary biologist proposes that complex biological systems appeared in this way. In fact, this is the same straw man assumption frequently made by Creationists in the past, and which has been likened to a Boeing 747 being assembled by a tornado blowing through a junkyard.
This is all there is to Dembski's main argument. He then makes a secondary argument in which he attempts to show that even if complex biological systems did evolve by undirected evolution, they could have only done so if a designer had fine-tuned the fitness function or inserted complex specified information at the start of the process.
The argument from fine-tuning of fitness functions appeals to a set of mathematical theorems called the "No Free Lunch" theorems. Although these theorems are perfectly sound, they do not have the implications which Dembski attributes to them. In fact they do not apply to biological evolution at all. All that is left of Dembski's argument is then the claim that life could only have evolved if the initial conditions of the Universe and the Earth were finely tuned for that purpose. This is an old argument, usually known as the argument from cosmological (and terrestrial) fine-tuning. Dembski has added nothing new to it.
Complex specified information (CSI) is a concept of Dembski's own invention which is quite different from any form of information used by information theorists. Indeed, Dembski himself has berated his critics in the past for confusing CSI with other forms of information. This critique shows that CSI is equivocally defined and fails to characterize complex structures in the way that Dembski claims it does. On the basis of this flawed concept, he boldly proposes a new Law of Conservation of Information, which is shown here to be utterly baseless.
Dembski claims to have made major contributions to the fields of statistics, information theory and thermodynamics. Yet his work has not been accepted by any experts in those fields, and has not been published in any relevant scholarly journals.
No Free Lunch consists of a collection of tired old antievolutionist arguments: god-of-the-gaps, irreducible complexity, tornado in a junkyard, and cosmological fine-tuning. Dembski attempts to give these old arguments a new lease of life by concealing them behind veils of confusing terminology and unnecessary mathematical notation. The standard of scholarship is abysmally low, and the book is best regarded as pseudoscientific rhetoric aimed at an unwary public which may mistake Dembski's mathematical mumbo jumbo for academic erudition.
In the theater of confusion, knowing the location of the
exits is what counts.
Mason Cooley, U.S.
aphorist
William Dembski's book No Free Lunch: Why Specified Complexity Cannot be Purchased without Intelligence1 is the latest of his many books and articles on inferring design in biology, and will probably play a central role in the promotion of Intelligent Design pseudoscience2 over the next few years. It is the most comprehensive exposition of his arguments to date. The purpose of the current critique is to provide a thorough critical examination of these arguments. Dembski himself has often complained that his critics have not fully engaged his arguments. I believe that complaint is unjustified, though I would agree that some earlier criticisms have been poorly aimed. This critique should lay to rest any such complaints.
As in his previous work, Dembski defines his own terms poorly, gives new meanings to existing terms (usually without warning), and employs many of these terms equivocally. His assertions often appear to contradict one another. He introduces a great deal of unnecessary mathematical notation. Thus, much of this article will be taken up with the rather tedious chore of establishing just what Dembski's arguments and claims really mean. I have tried very hard to find charitable interpretations, but there are often none to be found. I have also requested clarifications from Dembski himself, but none have been forthcoming.
Some time ago, I posted a critique3 of Dembski's earlier book, The Design Inference,4 to the online Metaviews forum, to which he contributes, pointing out the fundamental ambiguities in his arguments. His only response was to call me an "Internet stalker" while refusing to address the issues I raised, on the grounds that "the Internet is an unreliable forum for settling technical issues in statistics and the philosophy of science".5 He clearly read my critique, however, since he now acknowledges me as having contributed to his work (p. xxiv). While some of the ambiguities I drew attention to in that earlier critique have been resolved in his present volume, others have remained and many new ones have been added.
Some readers may dislike the frankly contemptuous tone that I have adopted towards Dembski's work. Critics of Intelligent Design pseudoscience are faced with a dilemma. If they discuss it in polite, academic terms, the Intelligent Design propagandists use this as evidence that their arguments are receiving serious attention from scholars, suggesting this implies there must be some merit in their arguments. If critics simply ignore Intelligent Design arguments, the propagandists imply this is because critics cannot answer them. My solution to this dilemma is to thoroughly refute the arguments, while making it clear that I do so without according those arguments any respect at all.
This critique assumes a basic knowledge of mathematics, probability theory and evolutionary theory on the part of the reader. In order to simplify some of my arguments, I have relegated many details to endnotes, which can be reached by numbered links. In some cases, assertions which are not substantiated in the body of the text are supported by arguments in endnotes.
Citations consisting merely of page numbers refer to pages in No Free Lunch.
Regrettably, some older browsers are unable to display a number of mathematical symbols which are used in this article. Netscape 4 is one of these.
In spring, when woods are getting green,
I'll try and tell
you what I mean.
Lewis Carroll, Through the
Looking-Glass (Humpty Dumpty)
For a book which is all about inferring design, it is surprising to discover that No Free Lunch does not clearly define the term. Design is equated with intelligent agency, but that term is not defined either. It is also described negatively, as the complement of necessity (deterministic processes) and chance (stochastic processes). However, deterministic and stochastic processes are themselves normally defined as mutually exhaustive complements: those processes which do not involve any uncertainty and those which do. So it is not clear what, if anything, remains after the exclusion of those two categories. Dembski associates design with the actions of animals, human beings and deities, but seems to deny the label to the actions of computers, no matter how innovative their output may be. What distinguishes an animal mind, say, from a computer? Obviously there are many physical differences. But why should the actions of one be considered design and not the other? The only explanation I can think of is that one is conscious and the other, presumably, is not. I conclude that, when he infers design, Dembski means that a conscious mind was involved.
It appears that Dembski considers consciousness to be a very special kind of process, which cannot be attributed to physical laws. He tells us that intelligent design is not a mechanistic explanation (pp. 330-331). Dembski would certainly not be alone in this view, though it is not at all clear what it means for a process to be non-mechanistic. It appears, however, that such a process is outside the realm of cause and effect. This raises all sorts of difficult philosophical questions, which I will not attempt to consider here. Even if we accept that non-mechanistic processes exist, Dembski gives us no reason to think that consciousness (or intelligent design) is the only possible type of non-mechanistic process. Yet he seems to assume this to be the case.
Even with this interpretation, we still run into a problem. In his Caputo example (p. 55), Dembski uses his design inference to distinguish between two possible explanations both involving the actions of a conscious being: either Caputo drew the ballots fairly or he cheated. Dembski considers only the second of these alternatives to be design. But both explanations involve a conscious agent. It could be said that, if Caputo drew fairly, he was merely mimicking the action of a mechanistic device, so this doesn't count. But that would raise the question of just what a mechanistic device is capable of doing. Is a sophisticated computer not capable of cheating? Indeed, is there any action of a human mind which cannot, in principle, be mimicked by a sufficiently sophisticated computer? If not, how can we tell the difference between conscious design and a computer mimicking design? Even if you doubt that in principle a computer could mimic all the actions of a human mind, consider whether it could mimic the actions of a rat, which Dembski also considers to be an intelligent agent capable of design (pp. 29-30).
To escape this dilemma, Dembski invokes the concept of derived intentionality: the output of a computer can "exhibit design", but the design was performed by the creator of the computer and not by the computer itself (pp. 223, 326). Whenever a phenomenon exhibits design, there must be a designer (a conscious mind, in my interpretation) somewhere in the causal chain of events leading to that phenomenon.
Dembski claims that contemporary science rejects design as a legitimate mode of explanation (p. 3). But he himself gives examples of scientists making inferences involving human agency, such as the inference by archaeologists that certain stones are arrowheads made by early humans (p. 71), and he labels these "design inferences". Is he claiming that such archaeologists are mavericks operating outside the bounds of mainstream science? I don't think so. I think that what Dembski really means to claim here is that contemporary science does not allow explanations involving non-mechanistic processes, and he is projecting his own belief that design is a non-mechanistic process onto contemporary science. But even if it's true that science does not allow explanations involving non-mechanistic processes, it certainly does allow the action of a mind to be inferred where no judgement need be made as to whether mental processes are mechanistic or not (and such a judgement is generally unnecessary).
An alternative interpretation of Dembski's claim might be that contemporary science rejects design as a legitimate mode of explanation in accounting for the origin of biological organisms. If this is what he means, then I reject the claim. If we were to discover the remains of an ancient alien civilization with detailed records of how the aliens manipulated the evolution of organisms, then I think that mainstream science would have little difficulty accepting this as evidence of design in biological organisms.
The word natural has been the source of much confusion in the debate over Intelligent Design. It has two distinct meanings: one is the complement of artificial, i.e. involving intelligent agency; the other is the complement of supernatural. Dembski tells us that he will use the word in the former sense: "...I am placing natural causes in contradistinction to intelligent causes" (p. xiii). He then goes on to say that contemporary science is wedded to a principle of methodological naturalism:
According to methodological naturalism, in explaining any natural phenomenon, the natural sciences are permitted to invoke only natural causes to the exclusion of intelligent causes. [p. xvi]
But the methodological naturalism on which most scientists insist requires only the rejection of supernatural explanations, not explanations involving intelligent agency. Indeed, we have just seen that contemporary science allows explanations involving human designers and, I argue, intelligent alien beings. Perhaps what Dembski really means is that methodological naturalism rejects the invocation of an "unembodied designer" (to use his term).6
Dembski introduces the term chance hypothesis to describe proposed explanations which rely entirely on natural causes. This includes processes comprising elements of both chance and necessity (p.15), as well as purely deterministic processes. It may seem odd to refer to purely deterministic hypotheses as chance hypotheses, but Dembski tells us that "necessity can be viewed as a special case of chance in which the probability distribution governing necessity collapses all probabilities either to zero or one" (p.71). Since Dembski defines design as the complement of chance and necessity, it follows that a chance hypothesis could equally well (and with greater clarity) be called a non-design hypothesis. And since he defines natural causes as the complement of design, we can also refer to chance hypotheses as natural hypotheses. Dembski's use of the term chance hypothesis has caused considerable confusion in the past, as many people have taken chance to mean purely random, i.e. all outcomes being equally probable. While Dembski's usage has been clarified in No Free Lunch, I believe it still has the potential to confuse. For the sake of consistency with Dembski's work, I will generally use the term chance hypothesis, but I will switch to the synonym natural hypothesis or non-design hypothesis when I think this will increase clarity.
Ignorance, Madam, pure ignorance.
Samuel Johnson (on being asked how he came to define a word
incorrectly in his dictionary)
In Chapter 2 of No Free Lunch, Dembski describes a method of inferring design based on what he calls the Generic Chance Elimination Argument. I'll refer to this method as the chance-elimination method. This method assumes that we have observed an event, and wish to determine whether any design was involved in that event.
The chance-elimination method is eliminative--it relies on rejecting chance hypotheses. Dembski gives two methods for eliminating chance hypotheses: a statistical method for eliminating individual chance hypotheses, and proscriptive generalizations, for eliminating whole categories of chance hypotheses.
3.1 Dembski's Statistical Method
The fundamental intuition behind Dembski's statistical method is this: we
have observed a particular event (outcome) E and wish to check whether a given
chance hypothesis H provides a reasonable explanation for this outcome.7 We
select an appropriate rejection region (a set of potential outcomes) R,
where E is in R, and calculate the probability of observing an outcome in this
rejection region given that H is true, i.e. P(R|
It is important to note that we need to combine the probabilities of all outcomes in an appropriate rejection region, and not just take the probability of the particular outcome observed, because outcomes can individually have small probabilities without their occurrence being significant. A rejection region which is appropriate for use in this way is said to be detachable from the observed outcome, and a description of a detachable rejection region is called a specification (though Dembski often uses the terms rejection region and specification interchangeably).
Consider Dembski's favourite example, the Caputo case (pp. 55-58). A Democrat politician, Nicholas Caputo, was responsible for making random draws to determine the order in which the two parties (Democrat and Republican) would be listed on ballot papers. Occupying the top place on the ballot paper was known to give the party an advantage in the election, and it was observed that in 40 out of 41 draws Caputo drew a Democrat to occupy this favoured position. In 1985 it was alleged that Caputo had deliberately manipulated the draws in order to give his own party an unfair advantage. The court which considered the allegation against Caputo noted that the probability of picking his own party 40 out of 41 times was less than 1 in 50 billion, and concluded that "confronted with these odds, few persons of reason will accept the explanation of blind chance."8
In conducting his own analysis of this event, Dembski arrives at the same probability as did the court, and explains the reasoning behind his conclusion. The chance hypothesis H which he considers is that Caputo made the draws fairly, with each party (D and R) having a 1/2 probability of being selected for the top place on each occasion.
Suppose that we had observed a typical sequence of 41 draws, such as the following:
DRRDRDRRDDDRDRDDRDRRDRRDRRRDRRRDRDDDRDRDD
The probability of this precise sequence occurring, given H, is extremely small: (1/2)41 = 4.55 × 10-13. However, unless that particular sequence had been predicted in advance, we would not consider the outcome at all exceptional, despite its low probability, since it was very likely that some such random looking sequence would occur. The historical sequence, on the other hand, contained just one R, and so looked something like this:
DDDDDDDDDDDDDDDDDDDDDDRDDDDDDDDDDDDDDDDDD
The second sequence (call it E) has exactly the same probability as the first one, i.e. P(E|H) = 4.55 × 10-13, but this time we would consider it exceptional, because the probability of observing so many Ds is extremely small. Any outcome showing as many Ds as this (40 or more Ds out of 41 draws) would have been considered at least as exceptional, so the probability we are interested in is the probability of observing 40 or more Ds. "40 or more Ds", then, is our specification, and, as it happens, there are 42 different sequences matching this specification, so P(R|H) = 42 × P(E|H) = 1.91 × 10-11, or about 1 in 50 billion. In other words, the probability we are interested in here is not the probability of the exact sequence we observed, but the probability of observing some outcome matching the specification. If we decide that this probability is small enough, we reject H, i.e. we infer that Caputo's draws were not fair. From now on, I will use the expression "small probability" to mean "probability below an appropriate probability bound".
In order to apply Dembski's method, we need to know how to select an appropriate specification and probability bound. Dembski expounds at length a set rules for selecting these parameters, but they can be boiled down to the following:
An appropriate specification is merely any one which can be derived (in some loose sense) from background knowledge which was available to us before observing the event in question. For example, when Dembski applies his method to the bacterial flagellum--his only biological example--he doesn't bother to use the technical rules that he developed earlier, or even to state the specification explicitly. Reading between the lines, his specification appears to be "anything with the function of an outboard rotary motor", and the only justification he gives for this specification is the statement that "humans developed outboard rotary motors well before they figured out that the flagellum was such a machine" (p. 289).
Dembski distinguishes between local and universal probability bounds. A local probability bound is one which is calculated for the purpose of a particular statistical test.9 The procedure for calculating such a bound is difficult and highly arbitrary (p. 83), so Dembski generally falls back on his universal probability bound. This is a very small number, 10-150 (i.e. 1 in 10150), which Dembski tells us is the smallest probability bound we need ever use, and which we can always use in the absence of a suitable local probability bound. He calculates it by multiplying the number of elementary particles in the Universe, the maximum possible number of elementary particle transitions (the inverse of the Planck time) per second, and the number of seconds in a billion times the current age of the Universe, to give a figure which, he argues, is the maximum number of probabilistic resources we need ever consider (p. 22):
1080 × 1045 × 1025 = 10150
Although I believe Dembski's statistical method is seriously flawed, the issue is not important to my refutation of Dembski's design inference. For the remainder of the main body of this critique, therefore, I will assume for the sake of argument that the method is valid. A discussion of the flaws will be left to an appendix. It is worth noting, however, that this method has not been published in any professional journal of statistics and appears not to have been recognized by any other statistician.
3.2 Proscriptive Generalizations
Dembski argues that we can eliminate whole categories of chance hypotheses by means of proscriptive generalizations. For example, he mentions the second law of thermodynamics, which proscribes the possibility of a perpetual motion machine. He describes the logic of such generalizations in terms of mathematical invariants (p. 274), though this adds absolutely nothing to his argument.
I accept that proscriptive generalizations can sometimes be made, and Dembski is welcome to use them to eliminate specific categories of chance hypotheses. But there is no proscriptive generalization that can rule out all chance hypotheses. Furthermore, his claim to have found a proscriptive generalization against Darwinian evolution of irreducibly complex systems is hollow (see 4.2 below).
3.3 The Argument From Ignorance
The conclusion of the Generic Chance Elimination Argument (step #8) is stated by Dembski as follows:
S [the subject making the inference] is warranted in inferring that E [the observed outcome] did not occur according to any of the chance hypotheses in {Hi}i in I and therefore that E exhibits specified complexity. [p. 73]
{Hi} is the set of all chance hypotheses which we believe "could have been operating to produce E" (p.72). Dembski also writes:
But what happens once some causal mechanism is found that accounts for a given instance of specified complexity? Something that is specified and complex is highly improbable with respect to all causal mechanisms currently known. Consequently, for a causal mechanism to come along and explain something that previously was regarded as specified and complex means that the item in question is in fact no longer specified and complex with respect to the newly found causal mechanism. [p. 330]
So, when we have eliminated all the chance hypotheses we can think of, we infer that the event was highly improbable with respect to all known causal mechanisms, and we call this specified complexity. Later Dembski tells us that an inference of specified complexity should lead inevitably to an inference of design. This being the case, it's not clear that the notion of specified complexity is serving any useful purpose here. Why not cut out the middleman and go straight from the Generic Chance Elimination Argument to design? Unfortunately, the introduction of this middleman does serve to cause considerable confusion, because Dembski equivocates between this sense of specified complexity and the sense assigned by his uniform-probability method of inference (which I will explain in section 6). To help clear up the confusion, I will refer to this middleman sense as eliminative specified complexity and to the other sense as uniform-probability specified complexity. Note that Dembski's specified complexity is not a quantity: an event simply exhibits specified complexity or it doesn't.
Thus we see that the chance-elimination method is purely eliminative. It tells us to infer design when we have ruled out all the chance (i.e. non-design) hypotheses we can think of. The design hypothesis says nothing whatsoever about the identity, nature, aims, capabilities or methods of the designer. It just says, in effect, "a designer did it".10
This type of argument is commonly known as an argument from ignorance or god-of-the-gaps argument. So there is no danger of misunderstanding, let me clarify that the accusation of argument from ignorance is not an assertion that those making the argument are ignorant of the facts, or even that they are failing to utilize the available facts. The proponents of an argument from ignorance are demanding that their explanation be accepted just because the scientific community is ignorant (at least partially) of how an event occurred, rather than because their own explanation has been shown to be a good one. Note that an argument from scientific ignorance differs from the deductive fallacy of argument from ignorance. The deductive fallacy takes the following form: "My proposition has not been proven false, so it must be true." The scientific argument from ignorance is not a deductive fallacy, because scientific inferences are not deductive arguments.
A god-of-the-gaps argument is an argument from ignorance in which the default hypothesis, to be accepted when no alternative hypothesis is available, is "God did it". Since Dembski tells us that his criterion only infers the action of an unknown designer, and not necessarily a divine one, the term designer-of-the-gaps might be more appropriate here, but I think it is reasonable to use the more familiar term, since the arguments follow the same eliminative pattern and Dembski has made it clear that the designer he has in mind is the Christian God. The god-of-the-gaps argument should not be confused with a god-of-the-gaps theology. The latter proposes that God's actions are restricted to those areas of which we lack knowledge, but does not offer this as an argument for the existence of God.
Dembski makes no good case for awarding such a privileged status to the design hypothesis. Why should we prefer "an unknown designer did it" to "unknown natural causes did it" or "we don't know what did it"? Furthermore, as we shall see, he tells us to accept design by elimination even when we do have some outline ideas for how natural causes might have done it.
3.4 Dembski's Responses to the Charge of Argument From Ignorance
Since arguments from ignorance are almost universally rejected as unsound by scientists and philosophers of science, Dembski is sensitive to the charge, but his attempts to avoid facing up to the obvious are mere evasions.
In response to this criticism, note first that even though specified complexity is established via an eliminative argument, it is not fair to say that it is established via a purely eliminative argument. If the argument were purely eliminative, one might be justified in saying that the move from specified complexity to a designing intelligence is an argument from ignorance (i.e., not X therefore Y). But unlike Fisher's approach to hypothesis testing, in which individual chance hypotheses get eliminated without reference to the entire set of relevant chance hypotheses that might explain a phenomenon, specified complexity presupposes that the entire set of relevant chance hypotheses has first been identified. This takes considerable background knowledge. What's more, it takes considerable background knowledge to come up with the right pattern (i.e., specification) for eliminating all those chance hypotheses and thus for inferring design. [p. 111]
Dembski is misconstruing the charge of argument from ignorance. It is not a question of how much knowledge we have utilized. Scientific knowledge is always incomplete. The chance-elimination method is purely eliminative because it makes no attempt to consider the merits of the design hypothesis, but merely relies on eliminating the available alternatives.
Design inferences that infer design by identifying specified complexity are therefore not purely eliminative. They do not merely exclude, but they exclude from an exhaustive set in which design is all that remains once the inference has done its work (which is not to say that the set is logically exhaustive; rather, it is exhaustive with respect to the inquiry in question--that is all we can ever do in science). Design inferences, by identifying specified complexity, exclude everything that might in turn exclude design. [p. 111]
Dembski's phrase "exhaustive with respect to the inquiry in question" is the sort of circumlocution in which he excels. It just means that the set is as exhaustive as we can make it. In other words, it's a fancy way to say we have eliminated all the chance hypotheses we could think of.
Design inferences therefore eliminate chance in the global sense of closing the door to all relevant chance explanations. To be sure, this cannot be done with absolute finality since there is always the possibility that some crucial probability distribution was missed. Nonetheless, it is not enough for the design skeptic merely to note that adding a new chance explanation to the mix can upset a design inference. Instead, the design skeptic needs to explicitly propose a new chance explanation and argue for its relevance to the case at hand. [pp. 67-68]
This is a clear argument from ignorance. Unless design skeptics can propose an explicit natural explanation, Dembski tells us, we should infer design.
For any event whatsoever, there exists a probability distribution that concentrates all probability on that event and thus assigns it a probability of one. It therefore makes no sense to criticize my generalization of Fisher's approach to hypothesis testing for failing to consider all possible chance hypotheses. [p. 70]
Dembski is not being criticized for failing to eliminate all possible chance hypotheses, but for adopting a purely eliminative method in the first place.
Archeologists infer that certain chunks of rock are arrowheads. Detectives infer that certain deaths were deliberate. Cryptographers infer that certain random looking symbol strings are actually encrypted messages. In every case they might be wrong, and further knowledge might reveal a plausible chance hypothesis behind what originally appeared to be designed. But such sheer possibilities by themselves do nothing to overturn our confidence in design inferences. [p. 71]
Yes, these design inferences are fallible, as are all scientific inferences. That is not the issue. The difference is that these inferences are not purely eliminative. The experts in question have in mind a particular type of intelligent designer (human beings) of which they know much about the abilities and motivations. They can therefore compare the merits of such an explanation with the merits of other explanations.
If Dembski wishes to defend god-of-the-gaps arguments as a legitimate mode of scientific inference, he is welcome to try. What is less welcome are his attempts to disguise his method as something more palatable.
3.5 Comparative and Eliminative Inferences
One way in which Dembski attempts to defend his method is to suggest that there is no viable alternative. The obvious alternative, however, is to consider all available hypotheses, including design hypotheses, on their merits, and then select the best of them. This is the position adopted by almost all philosophers of science, although they disagree on how to evaluate the merits of hypotheses. There seems no reason to treat inferences involving intelligent agents differently in this respect from other scientific inferences.
Dembski argues at some length against the legitimacy of comparative approaches to inference (pp. 101-110, 121n59). I will not address the specifics of the likelihood approach, on which he concentrates his fire. I leave that to its proponents. However, his rejection of comparative inferences altogether is clearly untenable. When we have two or more plausible hypotheses available--whether those involve intelligent agents or not--we must use some comparative method to decide between them.
Consider, for example, the case of the archaeologists who make inferences about whether flints are arrowheads made by early humans or naturally occurring pieces of rock. Let us take a borderline case, in which a panel of archaeologists is divided about whether a given flint, taken from a site inhabited by early humans, is an arrowhead. Now suppose that the same panel had been shown the same flint but told that it came from a location which has never been inhabited by flint-using humans, say Antarctica. The archaeologists would now be much more inclined to doubt that the flint was man-made, and more inclined to attribute it to natural causes. A smaller proportion (perhaps none at all) would now infer design. The inference of design, then, was clearly influenced by factors affecting the plausibility of the design hypothesis: whether or not flint-using humans were known to have lived in the area. The inference was not based solely on the elimination of natural hypotheses.
It is not my intention to argue for any particular method of comparing hypotheses. Philosophers of science have proposed a number of comparative approaches, usually involving some combination of the following criteria:
Other criteria often cited include explanatory power, track record, scope, coherence and elegance.
In opposing comparative methods, Dembski argues that hypotheses can be eliminated in isolation without there necessarily being a superior competitor. In practical terms, I agree, although I suspect that we would not eliminate a hypothesis unless we had in the back of our minds that there existed a plausible possibility of a better explanation. I do not deny that we can eliminate a hypothesis without having a better one in mind; I deny that we can accept a hypothesis without having considered its merits, as Dembski would have us do in the case of his design hypothesis. If all the available hypotheses score too badly according to our criteria, it may be best to reject all of them and just say "we don't know".
3.6 Reliability and Counterexamples
Dembski argues, on the basis of an inductive inference, that the chance-elimination method is reliable:
First (section 1.6) I offered an inductive argument, showing that in all cases where we know the causal history and where specified complexity was involved, an intelligence was involved as well. The inductive generalization that follows is that all cases of specified complexity involve intelligence. [p. 110]
Setting aside the question of whether such an induction would be justified if its premise were true, let's just consider whether or not the premise is true. Contrary to Dembski's assertion, his section 1.6 did not show anything of the sort. In fact, the only cases where we know that Dembski's method has been used to infer design are the two examples that Dembski himself describes: the Caputo case and the bacterial flagellum. And in neither of these cases has design been independently established.
Dembski wants us to believe that his method of inference is basically the same method already used in our everyday and scientific inferences of design. I have already argued that this is untrue. But even if we suppose, for the sake of argument, that our typical design inferences are indeed based on the sort of purely eliminative approach proposed by Dembski, then it is not difficult to find counterexamples, in which design was wrongly inferred because of ignorance of the true natural cause:
Fairy rings. These are rings of mushrooms caused by a fungus spreading through grass at a uniform rate from a given starting point. Mushrooms are manifested on the outer rim of the affected circle. Before the cause was known, these rings were often attributed to intelligent designers ("fairies"). If we take the chance hypothesis that the mushrooms were randomly located throughout a meadow (with a uniform probability distribution), the probability of them forming a neat circle is clearly small enough to justify the rejection of this hypothesis (by use of an appropriate local probability bound, if not Dembski's universal probability bound).12 Using Dembski's chance-elimination method, specified complexity (and hence design) would have been inferred erroneously.
Moon craters. On observing the major craters of the Moon, Johannes Kepler concluded that they were too circular to have occurred by chance, and so must have been created by inhabitants of the Moon. If we take the chance hypothesis that the craters were formed out of many individual hills, and that these hills were randomly distributed across the surface of the Moon, then the probability of them forming such good circles is clearly small enough to reject this hypothesis. Using Dembski's chance-elimination method, specified complexity (and hence design) would have been inferred, but we now know that these craters have a natural explanation--impacts from falling objects. I am indebted for this example to Dembski himself, who describes it13 but fails to notice that it provides a counterexample to his claim.
Perhaps Dembski would object that his claim ("in all cases where we know the causal history and where specified complexity was involved, an intelligence was involved as well") was only referring to cases where we observe specified complexity today. But, by definition, those are cases where we don't have a plausible natural explanation. If we had one, we would not infer specified complexity. If we know the causal history and it was not a natural cause, it must have been design. So, if this is what Dembski means, his claim is a tautology. It says that, whenever the cause is known to be design, the cause is design! You cannot make an inductive inference from a tautology.
It would do Dembski no good to claim that these are cases of derived design (see 6.1 below), e.g. that mushrooms and the solar system were originally designed. The chance-elimination method infers design in the particular event which is alleged to have small probability of occurring under natural causes. For example, in the case of the flagellum, Dembski claims that design was involved in the origin of the flagellum itself, and not just indirectly in terms of the Earth or the Universe having been designed.
The chance-elimination method is initially introduced in a simplified form called the Explanatory Filter. The criterion for the filter to recognize design is labelled the complexity-specification criterion. Unfortunately, the use of this simplified account has caused considerable confusion in the past, because it possesses two misleading features:
The description of the Explanatory Filter hardly mentions the concept of chance hypotheses, and implies that we need consider only one probability distribution. The flow chart for the filter (p. 13) should contain a loop, to be executed for each chance hypothesis. Many readers of Dembski's past work have been led to the erroneous conclusion that we only need to calculate the probability with respect to a uniform probability distribution.
The Explanatory Filter has separate nodes for complexity (which Dembski uses here as a synonym for improbability) followed by specification, as if these were two separate criteria. But, as we saw above, we cannot calculate the probability until we have formulated a specification. Many of Dembski's readers in the past have erroneously interpreted the filter as follows: note that the observed outcome is specified (in some sense) and then calculate the probability of that single outcome (when they should have calculated the probability of an entire rejection region).
Although Dembski has made some attempts to clarify the situation in No Free Lunch, his continued use of the Explanatory Filter in its highly misleading form is inexplicable. And the misdirection is not limited to the Explanatory Filter itself. It occurs elsewhere too, in statements such as this:
Determining whether an irreducibly complex system exhibits specified complexity involves two things: showing that the system is specified and calculating its probability... [p. 289]
He uses statistics as a drunken man uses lampposts--for
support rather than illumination.
Andrew Lang
(1844-1912), poet and novelist
It has been several years since Dembski first claimed to have detected design in biology by applying his method of inference. Yet until the publication of No Free Lunch, he had never provided or cited the details of any such application. Critics were therefore looking forward to seeing the long-promised probability calculation that would support the claim. While I, for one, did not expect a convincing calculation, even I was amazed to discover that Dembski has offered us nothing but a variant on the old Creationist "tornado in a junkyard"14 straw man, namely the probability of a biological structure occurring by purely random combination of components.
The only biological structure to which Dembski applies his method is the flagellum of the bacterium E. coli. As his method requires him to start by determining the set {Hi}of all chance hypotheses which "could have been operating to produce E [the observed outcome]" (p. 72), one might expect an explicit identification of the chance hypothesis under consideration. Dembski provides no such explicit identification, and the reader is left to infer it from the details of the calculation. Perhaps the reason Dembski failed to identify his chance hypothesis is that, when clearly named, it is so transparently a straw man. No biologist proposes that the flagellum appeared by purely random combination of proteins--they believe it evolved by natural selection--and all would agree that the probability of appearance by random combination is so minuscule that this is unsatisfying as a scientific explanation. Therefore for Dembski to provide a probability calculation based on this absurd scenario is a waste of time. There is no need to consider whether Dembski's calculation is correct, because it is totally irrelevant to the issue. Nevertheless, since Dembski does not state clearly that he has based his calculation on a hypothesis of purely random combination, I will describe the calculation briefly in order to demonstrate that this is the case.
Dembski tells us to multiply three partial probabilities to arrive at the probability of a "discrete combinatorial object":
pdco = porig × plocal × pconfig
plocal is the probability of a suitable collection of proteins being drawn from a set of existing proteins which includes the ones required. Dembski assumes that the proteins are randomly drawn from among the 4289 proteins coded for by E. coli's DNA, that 5 copies are needed of each of 50 different proteins (making 250 proteins altogether), and that, in each case, there are 10 different proteins that would be acceptable (i.e. there are 9 possible substitutes for the real protein. In effect, we have to make 250 draws, and at each draw we have a 500/4289 probability of picking a useful protein, giving an overall probability of (500/4289)250.
pconfig is the probability that, given the right collection of proteins, they will form a viable flagellum if arranged at random. Dembski aims to draw from a uniform probability distribution over all the possible ways of arranging the selected proteins:
Strictly speaking, the configuration probability for a discrete combinatorial object that exhibits some function is the ratio of all the ways of arranging its building blocks that preserve the function divided by all the possible ways whatsoever of arranging the building blocks. [pp. 294-295]
Since he can't calculate this directly, he uses an approximation that he calls a perturbation probability. We need not concern ourselves with the details.
porig is the probability of all the individual proteins forming by random combination of amino acids, and is again based on a perturbation probability.
Each of these probabilities individually is below Dembski's universal probability bound, so he does not proceed to multiply them.
Incidentally, Dembski errs in choosing to calculate a formation probability for the flagellum itself. He should have considered the formation of the DNA to code for a flagellum. If a flagellum appeared without the DNA to code for it, it would not be inherited by the next generation of bacteria, and so would be lost.
In order to justify his failure to calculate the probability of the flagellum arising by Darwinian evolution, Dembski invokes the notion of irreducible complexity, which, he argues, provides a proscriptive generalization against Darwinian evolution of the flagellum. Irreducible complexity was introduced into the Intelligent Design argument by biochemist Michael Behe. The subject has been addressed in great detail elsewhere, so I will not repeat all the objections.15 However, I would like to draw attention to a point which some readers of Behe have overlooked. Behe divided potential Darwinian pathways for the evolution of an irreducibly complex (hereafter IC) system into two categories: direct and indirect.16 The direct pathways are those in which a system evolves purely by the addition of several new parts that provide no advantage to the system until all are in place. All other potential pathways are referred to as indirect. Behe then argues that IC systems cannot evolve via direct pathways. But his direct pathways exclude two vital elements of the evolutionary process: (a) the evolution of individual parts of a system; and (b) the changing of a system's function over time, so that, even though a given part may have contributed nothing to the system's current function until the other parts were in place, it may well have contributed to a previous function. When it comes to indirect pathways, Behe has nothing but an argument from ignorance: no one has given a detailed account of such a pathway. The truth of this assertion has been contested, but it depends on just how much detail is demanded. Behe demands a great deal. He then asserts that the evolution of an IC system by indirect pathways is extremely improbable, but he has provided no argument to support this claim. It is merely his intuition.17
Dembski repeats the claim that the problem of explaining the evolution of IC molecular systems has "proven utterly intractable" (p. 246), but evolutionary explanations have now been proposed for several of the systems cited by Behe, including the blood-clotting cascade, the immune system, the complement system and the bacterial flagellum. The last of these is highly speculative, but is sufficient to refute the claim of utter intractability.18
What then has Dembski added to the debate over irreducible complexity? First, he has attempted to counter the objections of Behe's critics. I won't comment on these except to say that some of these critics appear to have misunderstood what Behe meant by irreducible complexity. This is unsurprising since his definition was vague and was accompanied by several misleading statements. Indeed, Behe himself has admitted that his definition was ambiguous.19 He has even tentatively proposed a completely new definition.20
Second, Dembski has proposed a new definition of his own, making three major changes:
Behe was very vague about how a system should be divided into parts. Sometimes he took individual proteins as his parts, but in the case of the bacterial flagellum he divided the system into just three parts, "a paddle, a rotor, and a motor", each consisting of multiple proteins (Darwin's Black Box, p. 72). Dembski requires the parts to be "nonarbitrarily individuated" (p. 285), which doesn't tell us much. What is significant, however, is that in the case of the bacterial flagellum he chooses individual proteins as his parts. In fact, he seems not to have even noticed that Behe divided the flagellum into only three parts:
Behe shows that the intricate machinery in this molecular motor--including a rotor, a stator, O-rings, bushings, and a drive shaft--requires the coordinated interaction of about thirty proteins and another twenty or so proteins to assist in their assembly. Yet the absence of any one of these proteins would result in the complete loss of motor function.... But a flagellum without its full complement of protein parts does not function at all. Behe therefore concludes that if the Darwinian mechanism is going to produce the flagellum, it will have to do so in one generation. [pp. 249-251]
Whereas Behe only considered a system to be IC if all of its parts were indispensable, Dembski considers a system IC if it has an irreducible core of indispensable parts.
Dembski has added two new conditions which must be met before a system can be considered evidence of intelligent design. In addition to being IC, the system's irreducible core must possess "numerous and diverse parts" and have the property of "minimal complexity and function" (p. 287). Both of these conditions are rather vague. "Numerous" and "diverse" are not quantified. The complexity of the system apparently need not be quite minimal, since, in the case of the bacterial flagellum, Dembski argues only that "the complexity of known flagella is not very different from the minimal complexity that such systems might in principle require" (p. 288, my emphasis).
The last of these changes is sure to create yet more confusion. It is no longer enough, according to Dembski, to show that a system is IC. It must also meet the two additional criteria. Yet, elsewhere in his book, Dembski continues to refer to irreducible complexity as a sufficient condition for inferring design:
In particular, the claim that the Darwinian mechanism can account for the full diversity of living forms will have to be rejected inasmuch as this mechanism is unable to generate the specified complexity inherent in--to take the most popular example--irreducibly complex biochemical systems (see chapter 5). [p. 324]
I can understand the temptation to use irreducibly complex as a shorthand term for irreducibly complex with an irreducible core which has numerous and diverse parts and exhibits minimal complexity and function, but Dembski should really have introduced a new term for the latter. From now on, when claiming to have found an example of irreducible complexity in nature, Intelligent Design proponents should specify which of the following definitions they have in mind: Behe's original definition; Behe's corrected version of his original definition; Behe's proposed new definition; Dembski's definition; or Dembski's definition plus the two additional criteria. I predict most will fail to do so. For the remainder of this article, I will use the term IC in the last of these senses. It should not be assumed that all the examples of IC systems offered by Behe necessarily meet Dembski's criteria. Dembski considers only the bacterial flagellum. Whether Behe's other example systems are IC in this new sense remains to be established.
Let us accept, for the sake of argument,
that Dembski's definition is tight enough to ensure that IC systems cannot
evolve by direct pathways. What has he said on the vital subject that
Behe failed to address--the subject of indirect pathways? The answer is
nothing. The crux of his argument is this:
To achieve an irreducibly complex system, the Darwinian mechanism has but two options. First, it can try to achieve the system in one fell swoop. But if an irreducibly complex system's core consists of numerous and diverse parts, that option is decisively precluded. The only other option for the Darwinian mechanism then is to try to achieve the system gradually by exploiting functional intermediates. But this option can only work so long as the system admits substantial simplifications. The second condition [that the irreducible core of the system is at the minimal level of complexity needed to perform its function] blocks this other option. Let me stress that there is no false dilemma here--it is not as though there are other options that I have conveniently ignored but that the Darwinian mechanism has at its disposal.[p. 287]
But there is indeed an option that Dembski has overlooked. The system could have evolved from a simpler system with a different function. In that case there could be functional intermediates after all. Dembski's mistake is to assume that the only possible functional intermediates are intermediates having the same function.
Dembski's failure to consider the possibility of a change of function is seen in his definition of irreducible complexity:
Definition ICfinal--A system performing a given basic function is irreducibly complex if it includes a set of well-matched, mutually interacting, non-arbitrarily individuated parts such that each part in the set is indispensable to maintaining the system's basic, and therefore original, function. The set of these indispensable parts is known as the irreducible core of the system. [p. 285]
There is no reason why a system's basic function should be its original one. The concepts of basic function and original function may not even be well-defined. If a system performs two vital functions, which is the basic one? The concept of an original function assumes there is an identifiable time at which the system came into existence. But the system may have a long history in which parts have come and gone, and functions have changed, making it impossible to trace back the origin of the system to one particular time. And what is a system? If two proteins start to interact in a beneficial way , do they immediately become a system? If so, we may have to trace the history of a system all the way back to the time when one it was just two interacting proteins.
There is a tendency among antievolutionists to think of biological systems as if they were like man-made machines, in which the system and its parts have been designed for one specific function and are difficult to modify for another function. But biological systems are much more flexible and dynamic than man-made ones.
A few other points are worth noting:
Changes of function are not an ad hoc idea thought up as a last-ditch attempt to solve a nasty problem. They are a fundamental feature of evolution. New systems do not just appear out of nowhere. Most systems will have evolved from an earlier system having a different function.
Changes of function can occur in two ways. First, a mutation may create a new capability. Second, a change in the environment may provide a new use for a system, e.g. a fish's fin starts to be used as a primitive leg in shallow water. In either case, the system may perform the new function very poorly at first, subsequently mutating to perform it better. Behe and Dembski both emphasize how well coordinated the parts of a system seem to be. But they may have been far less well coordinated in the past.
A system may have more than one function. In the example above, the fish's fin may continue to be used for swimming as well as clambering over submerged rocks.
There is no clear distinction between systems and parts. Any functional structure can be considered both a system in its own right and a part of a larger system. So we need not think in terms of a system acquiring a large number of parts consisting of individual proteins, as Dembski would have us do. A system may instead acquire a small number of sub-systems, each consisting of multiple proteins.
Instead of an IC system having to arise by the simultaneous combination of many parts, we now see that it can arise by the gradual acquisition of a few parts. This no longer sounds as unlikely as Behe and Dembski made it seem.
Before finishing this section, it might be useful to clear up a few more red herrings which Dembski introduces into his discussion of irreducible complexity.
Causal specificity. This is just another cover for the argument from ignorance:
Unless a concrete model is put forward that is detailed enough to be seriously criticized, then it is not going to be possible to determine the adequacy of that model. This is of course another way of saying that the scaffolding objection has yet to demonstrate causal specificity when applied to actual irreducibly complex biochemical systems. [p. 254]
In other words, until a sufficiently detailed natural hypothesis is provided, we should go ahead and infer design. It doesn't bother Dembski (or Behe who makes the same point) that their alternative hypothesis (design) lacks any details whatsoever.
Invariants. Dembski describes some geometrical problems which have no solution, and explains how the non-existence of a solution can be proven by showing that a certain property is invariant under transformation of the system. How is this relevant to irreducible complexity? Does Dembski use the invariance of some property to establish that IC systems cannot evolve? No, the property he claims to be invariant (under natural evolution) is the property of irreducible complexity itself. But the assertion that irreducible complexity cannot be produced by natural evolution was exactly the point which he was trying to establish. In other words, invariance does no work in establishing Dembski's conclusion. It is just another way of expressing that conclusion.
In trying to relate the subject of invariants to evolution, Dembski writes: "think of an effective invariant here as an insurmountable obstacle for the Darwinian mechanism" (p. 285). One has to wonder why he does not just use the expression "insurmountable obstacle" from the start, and skip the whole irrelevant discussion of invariants.
Specified complexity. Dembski likes to say that "irreducible complexity is a special case of specified complexity" (p. 289), as if this demonstrated the integration of two concepts into a coherent framework. But we have already seen that specified complexity is merely a label we apply when we have no plausible natural hypothesis to explain some event. So, to say that irreducible complexity is a case of specified complexity is just another way to repeat the claim that we have no natural explanation for the origin of the bacterial flagellum (which is the only biological system Dembski has shown to be IC in his sense).
Attempt the end, and never stand to doubt;
Nothing's so
hard, but search will find it out.
Robert Herrick
(1591-1674)
In recent years there has been a considerable growth of interest in evolutionary algorithms, executed on computers, as a means for solving optimization problems. As the name suggests, evolutionary algorithms are based on the same underlying principles as biological evolution: reproduction with random variations, and selection of the "fittest". Since they appear to demonstrate how unguided processes can produce the sort of functional complexity21 that we see in biology, they are a problem which Dembski needs to address. In addition, he tries to turn the subject to his advantage, by appealing to a set of mathematical theorems, known as the No Free Lunch theorems, which place constraints on the problem-solving abilities of evolutionary algorithms.
5.1 Black-Box Optimization Algorithms
We will be concerned here with a type of algorithm know as a black-box optimization (or search) algorithm. Such algorithms include evolutionary algorithms, but are not limited to them. The problems which black-box optimization algorithms solve have just two defining attributes: a phase space, and a fitness function defined over that phase space. In the context of these algorithms, phase spaces are usually called search spaces. Also the term fitness function is usually reserved for evolutionary algorithms, the more general term being objective function or cost function (maximizing an objective function is equivalent to minimizing a cost function). But I will adopt Dembski's terminology for the sake of consistency.
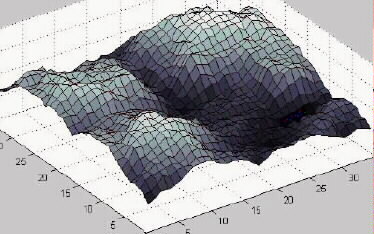
The phase space is the set of all potential solutions to the problem. It is generally a multidimensional space, with one dimension for each variable parameter in the solution. Most real optimization problems have many parameters, but, for ease of understanding, it is helpful to think of a two-dimensional phase space--one with two parameters--which can be visualized as a horizontal plane. The fitness function is a function over this phase space; in other words, for every point (potential solution) in the phase space the fitness function tells us the fitness value of that point. We can visualize the fitness function as a three-dimensional landscape where the height of a point represents its fitness (figure 1). Points on hills represent better solutions while points in valleys represent poorer ones. The terms fitness function and fitness landscape are used interchangeably.
Figure 1. A Fitness Landscape
An optimization algorithm is, broadly speaking, an algorithm for finding high points in the landscape. Being a black-box algorithm means that it has no knowledge about the problem it is trying to solve other than the underlying structure of the phase space and the values of the fitness function at the points it has already visited. The algorithm visits a sequence of points (x1, x2, ..., xm), evaluating the fitness, f(xi), of each one in turn before deciding which point to visit next. The algorithm may be stochastic, i.e. it may incorporate a random element in its decisions.
Evaluating the fitness function is typically a very computation-intensive process, possibly involving a simulation. For example, if we are trying to optimize the design of a road network, we might want the algorithm to run a simulation of daily traffic for each possible design that it considers. The performance of the algorithm is therefore measured in terms of the number of fitness function evaluations (m) needed to reach a given level of fitness, or the level of fitness reached after a given number of function evaluations. Each function evaluation can be thought of as a time step, so we can think in terms of the level of fitness reached in a given time. Note that we are interested in the best fitness value found throughout the whole time period, and not just the fitness of the last point visited.
There are three types of optimization algorithm of interest to us here:
Random search (also known as random sampling). This algorithm just selects each point at random (with a uniform probability distribution) out of all the points in the phase space.
Hill-climbers. A hill-climber visits some or all the points near to its current location, and moves to the highest one it finds. It never moves downwards. If it reaches the top of a hill, it gets stuck there, or it may begin a random search in the hope of finding a higher hill.
Evolutionary algorithms. An evolutionary algorithm maintains a population of individuals (usually randomly generated initially), that evolves according to rules of selection, recombination, mutation and survival. Each individual corresponds to a point in the phase space. A shared "environment" determines the fitness of each individual in the population. The fittest individuals are more likely to be selected for reproduction (retention or duplication), while recombination and mutation modify those individuals, yielding potentially superior ones.
Dembski adopts a very broad definition of evolutionary algorithm which includes all the optimization algorithms which we consider here, including random search (pp. 180, 229n9, 232n31).
Another term used by Dembski is blind search. He uses it in two senses. First it means a random walk, an algorithm which moves from one location in the phase space to another location selected randomly from nearby points (p. 190). Later he uses it to mean any search in which the fitness function has only two possible values: the point being evaluated either is or is not in a target area (p. 197). The usual (though not exclusive) meaning of blind search in the literature of evolutionary algorithms is as a synonym for black-box algorithm.22
5.2 Fine-Tuning the Fitness Function
Dembski recognizes that evolutionary algorithms can produce quite innovative results, but he argues that they can only do so because their fitness function has been fine-tuned by the programmer. In doing so, he alleges, the programmer has "smuggled" complex specified information or specified complexity into the result. (These two terms will be discussed later.)
Even so, there is something oddly compelling and almost magical about the way evolutionary algorithms find solutions to problems where the solutions are not like anything we have imagined. A particularly striking example is the "crooked wire genetic antennas" of Edward Altshuler and Derek Linden. The problem these researchers solved with evolutionary (or genetic) algorithms was to find an antenna that radiates equally well in all directions over a hemisphere situated above a ground plane of infinite extent. Contrary to expectations, no wire with a neat symmetric geometric shape solves this problem. Instead, the best solutions to this problem look like zigzagging tangles. What's more, evolutionary algorithms find their way through all the various zigzagging tangles--most of which don't work--to one that actually does. This is remarkable. Even so, the fitness function that prescribes optimal antenna performance is well-defined and readily supplies the complex specified information that an optimal crooked wire genetic antenna seems to acquire for free. [p. 221]
A similar claim is made regarding biological evolution:
Thus I submit that even if Darwinian evolution is the means by which the panoply of life on earth came to be, the underlying fitness function that constrains biological evolution would not be a free lunch and not a brute given, but a finely crafted assemblage of smooth gradients that presupposes much prior specified complexity. [p. 212]
These claims are based on a fundamental misconception of the role of the fitness function in an evolutionary algorithm. A fitness function incorporates two elements:
It reflects our objectives. If our aim is to design a bridge, we might need to decide what weight to give to a number of conflicting objectives such as traffic capacity, structural integrity, cost and environmental impact.
It encapsulates our relevant knowledge about the real world, in order to evaluate how well a potential solution meets our objectives.
In general, then, the fitness function defines the problem to be solved, not the way to solve it, and it therefore makes little sense to talk about the programmer fine-tuning the fitness function in order to solve the problem. True, there may be some aspects of the problem which are unknown, or where the programmer decides, for practical reasons, to simplify his model of the problem. Here the programmer could make decisions in such a way as to improve the performance of the algorithm. But there is no reason to think that this makes a significant contribution to the success of evolutionary algorithms.
In one of his articles, Dembski quotes evolutionary psychologist Geoffrey Miller in support of his claim that the fitness function needs to be fine-tuned:
And where exactly does design get built into an evolutionary or genetic algorithm? According to Miller, it gets built into the fitness function. He writes:
The fitness function must embody not only the engineer's conscious goals, but also her common sense. This common sense is largely intuitive and unconscious, so is hard to formalize into an explicit fitness function. Since genetic algorithm solutions are only as good as the fitness functions used to evolve them, careful development of appropriate fitness functions embodying all relevant design constraints, trade-offs and criteria is a key step in evolutionary engineering.23
But the engineer's goals, constraints, trade-offs, etc, are parameters of the problem to be solved. They must be carefully chosen to ensure that the evolutionary algorithm addresses the right problem, not to guide it to the solution of a given problem, as Miller tells us in the preceding paragraph:
If the fitness function does not realistically reflect the real-world constraints and demands that the phenotypic designs will face, the genetic algorithm may deliver a good solution to the wrong problem.24
It is other elements of the evolutionary algorithm which may have to be carefully selected if the algorithm is to perform well:
The trick in genetic algorithms is to find schemes that do this mapping from a binary biting to an engineering design efficiently and elegantly, rather than by brute-force.... The genetic operators copy and modify the genotypes from one generation to the next.... Getting the right balance between mutation and selection is especially important.... Finally, the evolutionary parameters [such as population size and mutation rate] determine the general context for evolution and the quantitative details of how the genetic operators work.... Deciding the best values for these parameters in a given application remains a black art, driven more by blind intuition and communal tradition than by sound engineering principles.24
A similar point is made by Wolpert and Macready:
Ultimately, of course, the only important question is, "How do I find good solutions for my given cost function f?" The proper answer to this question is to start with the given f, determine certain salient features of it, and then construct a search algorithm, a, specifically tailored to match those features. The inverse procedure--far more popular in some communities--is to investigate how specific algorithms perform on different f's. This inverse procedure is only of interest to the degree that it helps us with our primary procedure, of going from (features concerning) f to an appropriate a.25
Perhaps Dembski's confusion on this subject can be explained by his obsession with Richard Dawkins' Weasel program,26 to which he devotes a large part of his chapter on evolutionary algorithms. In that example, invented only to illustrate one specific point, the fitness function was indeed chosen in order to help the algorithm converge on the solution. That program, however, was not created to solve an optimization problem. The program had a specific target point, unlike real optimization algorithms, where the solution is unknown.
In the case of biological evolution, the situation is somewhat different, because the evolutionary parameters themselves evolve over the course of evolution. For example, according to evolutionary theory, the genetic code has evolved by natural selection. It is therefore not just good luck that the genetic code is so suited to evolution. It has evolved to be that way.
When Dembski talks about fine-tuning of the fitness function for biological evolution, what he really means is fine-tuning of the cosmological and terrestrial initial conditions, including the laws of physics. When these conditions are a given, as they are for practical purposes, they contribute to determining the fitness function. But Dembski argues that these conditions must have been selected from a set of alternative possibilities in order to make the evolution of life possible. When considered in this way, alternative sets of initial conditions should properly be considered as elements in another phase space, and not as part of the fitness function. Dembski sometimes refers to this as a phase space of fitness functions. One can understand what he means by this, but it is potentially confusing, not least because the fitness functions for biological organisms are not fixed, but evolve as their environment evolves.
We see then that Dembski's argument from fine-tuning of fitness functions is just a disguised version of the well-known argument from fine-tuning of cosmological and terrestrial initial conditions.27 Dembski lists a catalogue of cosmological and terrestrial conditions which need to be just right for the origin of life (pp. 210-211). This argument is an old one, and I won't address it here. The only new twist that Dembski gives to it is to cast the argument in terms of fitness functions and appeal to the No Free Lunch theorems for support. That appeal will be considered below, but first I want to make a couple of observations.
Dembski's two conclusions cannot both be true. On the one hand he is arguing that the initial conditions were fine-tuned to make natural evolution of life possible. On the other hand, he is arguing that natural evolution of life wasn't possible. Not that there's anything wrong with Dembski having two bites at the cherry. If one argument fails, he can fall back on the other. Alternatively Dembski might argue that the cosmic designer made the Universe almost right for the natural evolution of life, but left himself with a little work to do later.
If Dembski believes that the initial conditions for evolution were designed, the obvious thing to do would be to try applying his chance-elimination method to the origin of those conditions. I note that he doesn't attempt to do so.
5.3 The No Free Lunch Theorems
Dembski attempts to use the No Free Lunch theorems (hereafter NFL) of David Wolpert and William Macready28 to support his claim that fitness functions need to be fine-tuned. He presumably considers NFL important to his case, since he names his book after it. However, I will show that NFL is not applicable to biological evolution, and even for those evolutionary algorithms to which it does apply, it does not support the fine-tuning claim. I'll start by giving a brief explanation of what NFL says, making a number of simplifications and omitting details which need not concern us here.
NFL applies only to algorithms meeting the following conditions:
The algorithm must be a black-box algorithm, i.e. it has no knowledge about the problem it is trying to solve other than the underlying structure of the phase space and the values of the fitness function at the points it has already visited.
In principle, there must be a finite number of points in the phase space and a finite number of possible fitness values. In practice, however, continuous variables can be approximated by rounding to discrete values.
The algorithm must not visit the same point twice. This can be avoided by having the algorithm keep a record of all the points it has visited so far, with their fitness values, so it can avoid repeated visits to a point. This may not be practical in a real computer program, but most real phase spaces are sufficiently vast that revisits are unlikely to occur often, so we can ignore this issue.
The fitness function may remain fixed throughout the execution of the program, or it may vary over time in a manner which is independent of the progress of the algorithm. These two options correspond to Wolpert and Macready's Theorems 1 and 2 respectively. However, the fitness function may not vary in response to the progress of the algorithm. In other words, the algorithm may not deform the fitness landscape.29
The same algorithm can be used with any problem, i.e. on any fitness landscape, though it won't be efficient on all of them. In terms of a computer program, we can imagine inserting various alternative fitness function modules into the program. We can also imagine the set of all possible fitness functions. This is the vast set consisting of every possible shape of landscape over our given phase space. If there are S points in the phase space and F possible values of the fitness function, then the total number of possible fitness functions is FS, since each point can have any of F values, and we must allow for every possible permutation over the S points.
We are now in a position to understand what NFL says. Suppose we take an algorithm a1, measure its performance on every fitness function in that vast set of possible fitness functions, and take the average over all those performance values. Then we repeat this for any other algorithm a2. NFL tells us that the average performance will be the same for both algorithms, regardless of which pair of algorithms we selected. Since it is true for all pairs of algorithms, and since random search is one of these algorithms, this means that no algorithm is any better (or worse) than a random search, when averaged over all possible fitness functions. It even means that, averaged over all possible fitness functions, a hill-descending algorithm will be just as good as a hill-climbing algorithm at finding high points! (A hill-descender is like a hill-climber except that it moves to the lowest of the available points instead of the highest.)
This result seems incredible, but it really is true. The important thing to remember is the vital phrase "averaged over the set of all possible fitness functions". The vast majority of fitness functions in that set are totally chaotic, with the height of any two adjacent points being unrelated. Only a minuscule number of those fitness functions have the smooth rolling hills and valleys that we usually associate with a "landscape". In a chaotic landscape, there are no hills worthy of the name to be climbed. Furthermore, remember that every point which a hill-climber or descender peeks at counts as having been "found", even if the algorithm decides not to move there. So if a hill-descender happens to move adjacent to a very tall spike, the fitness value at that spike will be recorded and will count in the descender's final performance evaluation. A landscape picked at random from the set of all possible fitness functions will almost certainly be just a random mass of spikes (figure 2).

Figure 2. A Random Fitness "Landscape"
We can already see that the relevance of NFL to real problems is limited. The fitness landscapes of real problems are not this chaotic. This fact has been noted by a number of researchers:
In spite of the correctness of this "no-free-lunch theorem" (Wolpert and Macready 1997) the result is not too interesting. It is easy to see, that averaging over all different fitness functions does not match the situation of black-box optimization in practice. It can even be shown that in more realistic optimization scenarios there can be no such thing as a no-free-lunch theorem (Droste, Jansen, and Wegener 1999).30
5.4 The Irrelevance of NFL to Dembski's Arguments
NFL is not applicable to biological evolution, because biological evolution cannot be represented by any algorithm which satisfies the conditions given above. Unlike simpler evolutionary algorithms, where reproductive success is determined by a comparison of the innate fitness of different individuals, reproductive success in nature is determined by all the contingent events occurring in the lives of the individuals. The fitness function cannot take these events into account, because they depend on interactions with the rest of the population and therefore on the characteristics of other organisms which are also changing under the influence of the algorithm. In other words, the fitness function of biological organisms changes over time in response to changes in the population (of the same species and of other species), violating the final condition listed above. The same also applies to any non-biological simulations in which the individuals interact with each other, such as the competing checkers-playing neural nets which are discussed below.
It would do no good to suggest that the interactions between individuals could be modelled within the optimization algorithm, rather than in the fitness function. This is prevented by the black-box constraint, which stops the optimization algorithm having direct access to information about the environment.
This is similar to the problem of coevolving fitness landscapes raised by Stuart Kauffman (p. 224-227). Dembski's response to Kauffman, however, does not address my argument. Nothing that Dembski writes (p. 226) changes the fact that, in biological evolution, the fitness function at a given time cannot be determined independently of the state of the population, and therefore NFL does not apply.31
Moreover, NFL is hardly relevant to Dembski's argument even for the simpler, non-interactive evolutionary algorithms to which it does apply (those where the reproductive success of individuals is determined by a comparison of their innate fitness). NFL tells us that, out of the set of all mathematically possible fitness functions, there is only a tiny proportion on which evolutionary algorithms perform as well as they are observed to do in practice. From this, Dembski argues that it would be incredibly fortuitous for a suitable fitness function to occur without fine-tuning by a designer. But the alternative to design is not purely random selection from the set of all mathematically possible fitness functions. Fitness functions are determined by rules, not generated randomly. In the real world, these rules are the physical laws of the Universe. In a computer model, they can be whatever rules the programmer chooses, but, if the model is a simulation of reality, they will be based to some degree on real physical laws. Rules inevitably give rise to patterns, so that patterned fitness functions will be favoured over totally chaotic ones. If the rules are reasonably regular, we would expect the fitness landscape to be reasonably smooth. In fact, physical laws generally are regular, in the sense that they correspond to continuous mathematical functions, like "F = ma", "E = mc2", etc. With these functions, a small change of input leads to a small change of output. So, when fitness is determined by a combination of such laws, it's reasonable to expect that a small movement in the phase space will generally lead to a reasonably small change in the fitness value, i.e. that the fitness landscape will be smooth. On the other hand, we expect there to be exceptions, because chaos theory and catastrophe theory tell us that even smooth laws can give rise to discontinuities. But real phase spaces have many dimensions. If movement in some dimensions is blocked by discontinuities, there may still be smooth contours in other dimensions. While many potential mutations are catastrophic, many others are not.
Dembski might then argue that this only displaces the problem, and that we are incredibly lucky that the Universe has regular laws. Certainly, there would be no life if the Universe did not have reasonably regular laws. But this is obvious, and is not specifically a consequence of NFL. This argument reduces to just a variant of the cosmological fine-tuning argument, and a particularly weak one at that, since the "choice" to have regular laws rather than chaotic ones is hardly a very "fine" one.
Although it undermines Dembski's argument from NFL, the regularity of laws is not sufficient to ensure that real-world evolution will produce functional complexity. Dembski gives one laboratory example where replicating molecules became simpler (the Spiegelman experiment, p. 209). But it does not follow that this is always so. Dembski has not established any general rule. I would suggest that, because the phase space of biological evolution is so massively multidimensional, we should not be surprised that it has produced enormous functional complexity.
Operator... Give me Information.
Song by William Spivery
Dembski tells us that he has two different arguments for design in nature. As well as attempting to show that there exist in nature phenomena which Darwinian evolution does not have the ability to generate (such as the bacterial flagellum), Dembski also deploys another argument. Even if Darwinian evolution did have that ability, he argues, it could only have it by virtue of there having been design involved in the selection of the initial conditions underlying evolution.
The Darwinist therefore objects that "real life" Darwinian evolution can in fact generate specified complexity without smuggling it in after all. The fitness function in biological evolution follows directly from differential survival and reproduction, and this, according to the Darwinist, can legitimately be viewed as a "free lunch".... If this objection is conceded, then the only way to show that the Darwinian mechanism cannot generate specified complexity is by demonstrating that the gradients of the fitness function induced by differential survival and reproduction are not sufficiently smooth for the Darwinian mechanism to drive large-scale biological evolution. To use another Dawkins metaphor, one must show that there is no gradual way to ascend "Mount Improbable." This is a separate line of argument and one that I shall take up in the next chapter [which addresses irreducible complexity and the bacterial flagellum]. Here, however, I want to show that this concession need not be granted and that the displacement problem does indeed undercut Darwinism. [p. 208]
This is an argument for what I will call derived design. (Dembski uses the term derived intentionality.) It does not argue for design in a particular event (such as evolution of some structure), but merely argues that design must have been involved at some point or other in the causal chain of events leading to some phenomenon that we observe.
We have already seen this argument cast in terms of fine-tuning of fitness functions. Dembski also casts it in terms of specified complexity. Earlier, specified complexity was introduced as something to be inferred when we had eliminated all the natural hypotheses we could think of to explain an event. But now Dembski is telling us that, even if we cannot eliminate Darwinian evolution as an explanation, we should still make an inference of derived design if we observe specified complexity. Clearly, then, this is a different meaning of specified complexity. This new meaning is an observed property of a phenomenon, not an inferred property of an event. It indicates that the phenomenon has a complex (in a special sense) configuration. This property also goes by the name of complex specified information (CSI).
Note that this is another purely eliminative method; it infers design from the claimed absence of any natural process capable of generating CSI. If the claim were true, it could be considered a proscriptive generalization, but we will see that the claim has no basis whatsoever.
6.2 Complex Specified Information (CSI)
Dembski devises his own measure of how complex a phenomenon's configuration is, and calls it specified information (which I'll abbreviate to SI). He calculates this measure by choosing a specification (as described in 3.1 above) and then calculating the probability of an outcome matching that specification as if the phenomenon was generated by a process having a uniform probability distribution. A uniform probability distribution is one in which all possible outcomes (i.e. configurations) have the same probability, and Dembski calculates the SI on this basis even if the phenomenon in question is known not to have been generated by such a process. (This will be considered more carefully in the next section.) The probability calculated in this way is then converted into "information" by applying the function I(R) = -log2P(R), i.e. the information is the negation of the logarithm (base 2) of the probability, and he refers to the resulting measure as a number of bits.
If the SI of a phenomenon exceeds a universal complexity bound of 500 bits, then Dembski says that the phenomenon exhibits complex specified information (or CSI).32 The universal complexity bound is obtained directly from Dembski's universal probability bound of 10-150, since -log2(10-150) is approximately 500. Dembski also refers to CSI as specified complexity, using the two terms interchangeably. As noted above, this meaning of specified complexity is different from the one we encountered earlier. I'll call it uniform-probability specified complexity. To be clear: eliminative specified complexity is an inferred attribute of an event, indicating that we believe the event was highly improbable with respect to all known causal mechanisms; uniform-probability specified complexity (or CSI) is an observed attribute of a phenomenon, indicating that the phenomenon has a "complex" configuration, without regard to how it came into existence. We will see that Dembski's notion of "complexity" is very different from our normal understanding of the word.
6.3 Evidence For The Uniform-Probability Interpretation
The fact that the probability used to calculate SI is always based on a uniform probability distribution is extremely important. Dembski uses a uniform (or "purely random") distribution even if the phenomenon is known to have been caused by a process having some other probability distribution. Since this is not explicitly stated by Dembski, and may seem surprising, I will present several items of evidence to justify my interpretation.
As argued in 6.1 above, Dembski's derived design argument implies that SI is an observed property of a phenomenon, which allegedly allows us to infer design in the distant past regardless of what subsequent natural processes might have led to the phenomenon. There are therefore no relevant probability distributions under which to calculate the probability for SI. We must use some default probability distribution, and a uniform distribution seems to be the only candidate.
Here Dembski specifically mentions a uniform probability distribution:
For instance, in Dawkins's METHINKS-IT-IS-LIKE-A-WEASEL example (see section 4.1), the phase space consists of all sequences 28 characters in length comprising upper case Roman letters and spaces (spaces being represented by bullets). A uniform probability on this space assigns equal probability to each of these sequences--the probability value is approximately 1 in 1040 and signals a highly improbable state of affairs. It is this improbability that corresponds to the complexity of the target sequence and which by its explicit identification specifies the sequence and thus renders it an instance of specified complexity (though as pointed out in section 4.1, we are being somewhat loose in this example about the level of complexity required for specified complexity--technically, the level of complexity should correspond to the universal probability bound of 1 in 10150). [p. 188-189]
This seems clear. However, Dembski goes on to say that "E [the evolutionary algorithm] has in fact not generated specified complexity at all but merely shifted it around" (p. 195). (By this point Dembski has switched to another version of the Weasel program, but the change is inconsequential.) Although he fails to state it explicitly, the implication is that the outcome does exhibit specified complexity, though this was "smuggled" into the program and not generated by it.
My next piece of evidence comes from Dembski's accounts of Tom Schneider's binding site simulation33 (pp. 213-218) and the checkers-playing neural nets of Kumar Chellapilla and David Fogel (pp. 221-223), which I will describe later. These programs have a high probability of producing a good solution (as has been confirmed to me by their programmers). Since Dembski asserts that the outcomes exhibited specified complexity (CSI), which implies a low probability of producing a specified result (a good solution), it follows that he must have been estimating the probability with respect to some probability distribution other than the true one. The only apparent candidate is a uniform probability distribution.
One of Dembski's examples (pp. 6-9) is an event from the film Contact, starring Jodie Foster, in which astronomers at SETI (the Search for Extraterrestrial Intelligence) detect a radio signal of extraterrestrial origin. The signal comprises a sequence of 1126 beats and pauses, representing the first 25 prime numbers: 2, 3, 5, 7, ..., 101. Each prime number is represented by a sequence of beats equal to the number, with consecutive numbers separated by a pause. Converting the beats to 1s and the pauses to 0s, the signal can be represented by a sequence of 1126 binary digits (bits), beginning "110111011111011111110...". The fictional astronomers immediately recognized this signal as having an intelligent origin.
Dembski tells us that the SETI sequence exhibits specified complexity (p. 359). On pp. 143-144 he gives an abbreviated 1000-bit version of this sequence, telling us that it has a probability of 1 in 21000, giving SI of over 500 bits (presumably 1000 bits). The latter example is based on a known cause (intelligent agency or coin tossing), but presumably the sequence has the same SI regardless of its cause. After all, we don't know the true cause of the SETI sequence, yet Dembski still tells us it exhibits specified complexity. It is very unlikely that the SETI sequence was produced by the equivalent of coin tossing. A much more likely scenario is that the extraterrestrials have programmed a computer to generate the sequence automatically. In that case, we're back to the same sort of situation as the Weasel program. Furthermore, if we were considering all relevant chance hypotheses, we should consider the possibility that the two alternative outcomes of each beat/pause were not equally likely. In the absence of any other information, the best estimate of the probabilities of beat and pause would be 1102/1126 and 24/1126 respectively, since we observed 1102 beats and 24 pauses. With these probabilities (and still assuming that each beat/pause is independent of the others), the probability of receiving the SETI sequence would be (1102/1126)1102 × (24/1126)24 = 3.78 × 10-51, considerably larger than the universal probability bound of 10-150. I therefore conclude that Dembski calculates the SI of the SETI sequence on the basis of the beats and pauses having equal probability (1/2) and that the sequence exhibits 1126 bits of SI.
Finally, I must mention a counterexample to my uniform-probability interpretation. Dembski considers the case of a gene, T-urf13, which occurs in a particular strain of maize (pp. 218-219). This gene codes for a protein product called URF13. In determining whether URF13 exhibits CSI, Dembski starts by calculating a probability of 2083, on the grounds that the minimal functional size of URF13 is 83 amino acids and that there are 20 possible amino acids. So he is assuming that URF13 is drawn from a uniform probability distribution over the space of all possible sequences of 83 amino acids. He then points out that the probability is really higher than this as we must allow for the possibility of other sequences having the same function as URF13, i.e. other sequences matching the same specification. So far, then, this supports the uniform-probability interpretation. Further down the page, however, he argues that the probability on which SI must be based is higher still:
What if any way we sliced it, the improbabilities computed turned out to be less than the universal probability bound? Would that demonstrate that CSI had been naturalistically generated? No. First off, there is no reason to think that non-protein-coding gene segments themselves are truly random--as noted above, T-urf13, which is composed of such segments, is homologous to ribosomal RNA. So it is not as though these segments were produced by sampling an urn filled with loosely mixed nucleic acids. What's more, it is not clear that recombination itself is truly random. [p. 219]
Now Dembski is saying that we shouldn't just calculate SI based on a uniform probability (urn) model, but should take into account the causal processes which we think are operating. But this contradicts the computer examples given above, where we knew the actual causal process (execution of a computer program) and that process gave a specified result with high probability, yet Dembski told us that the result exhibited CSI anyway.
Although the evidence is inconclusive, it seems to predominantly favour the uniform-probability interpretation, and that is the one that I will consider hereafter. But let me briefly look at the alternatives:
SI is based on the probability with respect to the true causal process responsible for the event. This would make SI useless for the purpose of making inferences about the cause of a phenomenon. We would need to know the cause in order to infer the cause! Furthermore, it would be meaningless to say that a designed phenomenon exhibits CSI, since there is no probability distribution with respect to which we can calculate the SI of a designed phenomenon (as Dembski tells us that design is not a probabilistic process). This interpretation is clearly untenable.
SI is based on our best understanding of the causal processes which we think might underlie the event which gave rise to the observed phenomenon. But this is just the chance-elimination method again. We calculate the SI under the best chance hypothesis we can think of (the one conferring the highest probability on a detachable rejection region). If the SI under this chance hypothesis is high enough (probability low enough), we reject this chance hypothesis and infer design. By implication, we have already considered and rejected all the inferior chance hypotheses that we could think of (those conferring only lower probabilities on detachable rejection regions). In that case, the assertion that a phenomenon exhibits CSI is merely an assertion that it is improbable under all the chance hypotheses we can think of. In other words, this is the same argument from ignorance which was addressed earlier.
If Dembski insists that he has only one method of design inference and that it's the chance-elimination method, then he needs to explain away the exhibits above and justify his introduction of the terms "complexity" and "information". The chance-elimination method uses a statistical (probabilistic) technique for eliminating hypotheses. This has nothing to do with complexity or information. Transforming probabilities by applying the trivial function I = -log2P does not magically convert them into complexity or information measures. It only serves to obfuscate the nature of the argument.
My guess is that Dembski has failed to notice that he has two different methods. One reason for his confusion may be that all the chance hypotheses he ever considers in his examples are ones which give rise to a uniform probability distribution, with the sole exception of one trivial case (p. 70).
Dembski also seems to consider uniform probability distributions "privileged" in some sense (p. 50). Referring to the phase space of an optimization algorithm, he writes:
Moreover, such spaces typically come with a uniform probability that is adapted to the topology of the phase space. What this means is that Ω [the phase space] possesses a uniform probability measure U adapted to the metric on Ω so that geometrically congruent pieces of Ω get assigned identical probabilities (see section 2.2). [p. 188]
But a phase space (as the search space of an optimization algorithm) does not come with a probability distribution attached. It is simply a space of possible solutions which we are interested in searching.34
Although basing SI on a uniform probability distribution helps to make it independent of the causal process which produced the phenomenon, it cannot make it completely independent. Given a phase space (or reference class of possibilities, as Dembski calls it), there is only one possible uniform distribution, the one in which all outcomes have equal probability. But how do we choose a phase space? In the case of the SETI sequence it may seem obvious that the relevant phase space is the space of all possible bit sequences of length 1126. But why should we assume that the sequence was drawn from a space of 1126-bit sequences, and not sequences of variable length? Why should we assume that beat and pause were the only two possible values? The supposed extraterrestrials could have chosen to transmit beats of varying amplitudes.
Similar problems arise elsewhere. On p. 166, Dembski calculates the complexity of the word METHINKS as -log2(1/278) = 38 bits.35 This is based on a phase space of strings of 8 characters where each character has 27 possibilities (26 letters in the alphabet plus a space). He does not consider the possibility of more or fewer than 8 characters. So clearly Dembski has a rule that we should only consider possible permutations of the same number of characters (or components) as we actually observed. No justification is given for such a rule, and it still leaves us with an arbitrary choice to make regarding the unit of permutation. In the case of METHINKS, it might be argued that the only sensible unit of permutation is the character. But in other cases we have to make a choice. In a sentence, should we consider permutations of characters or of words? In a genome, should we consider permutations of genes, codons, base pairs or atoms?
Even more problematical is the range of possible characters. Here Dembski has chosen the 26 capital letters and a space as the only possibilities. But why not include lower case letters, numerals, punctuation marks, mathematical symbols, Greek letters, etc? Just because we didn't observe any of those, that doesn't mean they weren't real possibilities. And if we are to consider only the values that we actually observed, why did Dembski include all 26 letters of the alphabet? Many of those letters were not observed in the word METHINKS or even in the longer sentence in which it was embedded. Perhaps Dembski is relying on knowledge of the causal process which gave rise to the word, knowing that the letters were drawn from a collection of 27 Scrabble tiles, say. But to rely on knowledge of the causal process makes the criterion useless for those cases where we don't know the cause. And the whole purpose of the criterion was to enable us to infer the type of causal process (natural or design) when it is unknown.
The selection of an appropriate phase space is not such a problem in standard Shannon information theory,36 because we are concerned there with measuring the information transmitted (or produced) by a process. Dembski, on the other hand, wants to measure the information exhibited by a given phenomenon, and from that make an inference about the causal process which produced the phenomenon. This requires him to choose a phase space without knowing the causal process, the result being that his phase spaces are arbitrary.
Dembski devotes a section of his book (pp. 133-137) to the problem of selecting a phase space, but fails to resolve the problem. He argues that we should "err on the side of abundance and include as many possibilities as might plausibly obtain within that context" (p. 136). But this means that we err on the side of overestimating the amount of information exhibited by a phenomenon, and so err on the side of falsely inferring design. This is hardly reasonable for a method which is supposed to infer design reliably. In any case, Dembski doesn't follow his own advice. We just saw in the METHINKS example that he chose a space based on only 27 characters--hardly the maximum plausible number given no knowledge of the causal process.
Given that SI is based on a uniform probability distribution, there is little doubt that CSI exists in nature. Indeed, all sorts of natural phenomena can be found to exhibit CSI if a suitable phase space is chosen. Take the example mentioned earlier of craters on the Moon. If we take the space of all theoretically possible lunar landscapes and randomly pick a landscape from a uniform distribution over that space, then the probability of obtaining a landscape exhibiting such circular formations as we actually observe on the Moon is extremely small, easily small enough to conclude that the actual lunar landscape exhibits CSI. Even the orbits of the planets exhibit CSI. If a planetary orbit were randomly picked from a uniform probability distribution over the space of all possible ways of tracing a path around the Sun, then the probability of obtaining such a smooth elliptical path as a planetary orbit is minuscule.
6.5 The Law of Conservation of Information
The Law of Conservation of Information (hereafter LCI) is Dembski's formalized statement of his claim that natural causes cannot generate CSI; they can only shuffle it from one place to another. The LCI states that, if a set of conditions Y is sufficient to cause X, then the SI exhibited by Y and X combined cannot exceed the SI of Y alone by more than the universal complexity bound, i.e.
I(Y&X) <= I(Y) + 500
where I(Y) is the amount of SI exhibited by Y. (I have made Y antecedent to X, rather than the other way around, for the sake of consistency with Dembski's explanation on pages 162-163.)
Despite its name, the LCI is not a conservation law. Since Dembski acknowledges that small amounts of SI (less than 500 bits) can be generated by chance processes (pp. 155-156), the LCI cannot be construed as a conservation law in any reasonable sense of the term. It is, rather, a limit on how much SI can be generated.
My discussion of the LCI below will be based on my uniform-probability interpretation of SI. However, in case Dembski rejects this interpretation, let me first consider what the LCI would mean if SI is based on the true probabilities of events. It would then be just a disguised version of Dembski's old Law of Small Probabilities, from The Design Inference, which states that specified events of small probability (less than 10-150) do not occur. He has merely converted probability to "information" by applying the function I = -log2P to each side of an inequality, with the probabilities conditioned on the occurrence of Y. To see this, let X be a specified event which has occurred as a result of Y. Then, by the Law of Small Probabilities,
In this case, the LCI is just a probability limit and has nothing to do with information or complexity in any real sense. I will therefore not consider this interpretation any further.
6.6 Counterexample: Checkers-Playing Neural Nets
My first counterexample to the LCI is one which Dembski bravely introduces, namely the evolving checkers-playing neural nets of Chellapilla and Fogel (pp. 221-223).37 I'll start with a brief description of the evolutionary algorithm. Neural nets were defined by a set of parameters (the details are unimportant) which determined their strategy for playing checkers. At the start of the program run, a population of 15 neural nets was created with random parameters. They had no special structures corresponding to any principles of checkers strategy. They were given just the location, number and types of pieces--the same basic information that a novice player would have on his/her first game. In each generation, the current population of 15 neural nets spawned 15 offspring, with random variations on their parameters. The resulting 30 neural nets then played a tournament, with each neural net playing 5 games as red (moving first) against randomly selected opponents. The neural nets were awarded +1 point for a win, 0 for a draw and -2 for a loss. Then the 15 neural nets with the highest total scores went through to the next generation. I'll refer to the (+1, 0, -2) triplet as the scoring regime, and to the survival of the 15 neural nets with the highest total score as the survival criterion.
The neural nets produced by this algorithm were very good checkers players, and Dembski assumes that they exhibited specified complexity (CSI). He gives no justification for this assumption, but it seems reasonable given the uniform-probability interpretation. Presumably the specification here is, broadly speaking, the production of a good checkers player, and the phase space is the space of all possible values of a neural net's parameters. If the parameters were drawn randomly, the probability of obtaining a good checkers player would be extremely low. Since the output of the program exhibited CSI, Dembski needs to show that there was CSI in the input. To his credit, Dembski doesn't take the easy way out and claim that the CSI was in the computer or in the program as a whole. The programming of the neural nets was quite independent of the evolutionary algorithm. Instead Dembski claims that the CSI was "inserted" by Chellapilla and Fogel as a consequence of their decision to keep the "criterion of winning" constant from one generation to the next! But a constant criterion is the simplest option, not a complex one, and the idea that such a straightforward decision could have inserted a lot of information is absurd.
As we saw earlier, the fitness function reflects the problem to be solved. In this case, the problem is to produce neural nets which will play good checkers under the prevailing conditions. Since the conditions under which the evolved neural nets would be playing were (presumably) unknown at the time the algorithm was programmed, it might be argued that the choice of winning criterion was a free one. The programmers could therefore have chosen any criterion they liked. Nevertheless, the natural choice in such a situation is to choose the simplest option. In choosing a constant winning criterion, that is what the programmers did. Since they had no reason to think the neural nets would find themselves in a tournament with variable winning conditions, there was no reason to evolve them under such conditions.
Contrary to Dembski's assertion that the choice of a constant criterion "is without a natural analogue", the natural analogue of the constant winning criterion is the constancy of the laws of physics and logic.
Also, their choice is without a natural analogue. Chellapilla and Fogel kept constant their criterion for "tournament victory." For biological systems, the criterion for "tournament victory" will vary considerably depending on who is playing in the tournament. [p. 223]
It's not clear what Dembski means by "the criterion for tournament victory". However, the fact that a biological system's success depends on who is "playing in the tournament" certainly does have an analogue in Chellapilla and Fogel's algorithm. The success of a neural net was dependent on which other neural nets were playing in the tournament.
Before considering some further objections to Dembski's claim, I need to decide what he means by "criterion of winning". Does he mean just the scoring regime? Or does he mean the entire set of tournament rules: the selection of opponents, the scoring regime and the survival criterion? For brevity, I will consider only the scoring regime, but similar arguments can be made in respect of the other elements of the tournament rules.
Dembski insists that the SI "inserted" by Chellapilla and Fogel's choice is determined with respect to "the space of all possible combinations of local fitness functions from which they chose their coordinated set of local fitness functions". It's not clear what Dembski means by fitness functions here. As we've seen, in a situation where the success of an individual depends on its interactions with other individuals in the population (in this case the population of neural nets), the fitness function varies as the population varies, since the fitness of an individual is relative to its environment, which includes the rest of the population. Dembski seems to recognize this, since he writes:
There is not even a fitness function defined over the entire space of checker-playing neural nets. Instead, each collection of 30 neural nets gets its own local fitness function that assigns fitness depending on how a neural net fares in a tournament with other neural nets... [p. 222]
When Dembski refers to a "local fitness function" here, he apparently means the fitness function of one particular generation.38 But, contrary to Dembski's claim, the sequence of fitness functions was not "coordinated" by Chellapilla and Fogel. It was dependent on the evolution of the population of neural nets. So it makes no sense to talk about Chellapilla and Fogel selecting from "the space of all possible combinations of local fitness functions". It would make some sense, however, to talk about them selecting from the phase space of all possible time-dependent scoring regimes (one triplet per generation), and I will assume that this is what Dembski means.
For the reasons already given, it is hardly reasonable to consider the scoring regime to have been selected from such a phase space. Nevertheless, even if we do so, the amount of SI inserted by Chellapilla and Fogel's choice was minimal. This is because the SI must be based on a rejection region consisting of all the possible time-dependent scoring regimes which would have performed as well as Chellapilla and Fogel's or better. Suppose that, instead of using a constant scoring regime, the program randomly generated a new scoring triplet (W, D, L) for each generation, subject only to the constraint that W > D > L. This constraint is not an artificial imposition; it is a characteristic of the problem to be solved. If the problem was to find good players for suicide checkers (where the object of the game is to "lose"), the constraint would be L > D > W. Since SI is based on a uniform probability distribution, the values of W, D and L would be drawn from a uniform probability distribution over some continuous range, say [+2, -2]. We are only concerned with the relative values of W, D and L, so the choice of range is arbitrary and could itself be made randomly at the start of each run. The question then is how often such a program would perform as well as the original, i.e. would produce as good players in the same amount of time. If, for the sake of example, the revised program performs as well as the original on 1/8 of occasions (out of a sufficiently large sample), this means that 1 in 8 time-dependent regimes performs as well as Chellapilla and Fogel's. The SI of Chellapilla and Fogel's regime would then be only -log2(1/8) = 3 bits. For Dembski to maintain his claim that this choice inserted CSI, the onus is on him to show that the proportion of regimes performing as well as Chellapilla and Fogel's is less than 1 in 10150, and that seems very unlikely to be the case.
In case Dembski has a problem with even the natural constraint that I suggested above, let's consider an alternative which has no prior constraints. Suppose that, at the start of each run, the program draws 6 random numbers from an arbitrary range (as above). Call these numbers W-, W+, D-, D+, L-, L+. For each generation, the program generates a new scoring triplet (W, D, L), selecting these parameters randomly from uniform probability distributions over the ranges [W-, W+], [D-, D+] and [L-, L+] respectively. Many program runs will fail to produce good checkers players at all (though they may produce players who are good at playing suicide checkers or good at forcing a draw). However, on a small proportion of runs (1/720 on average), it will just so happen that W+ > W- > D+ > D- > L+> L-, and on these runs we can expect the program to produce good checkers players.39 So, if we run the program enough times, the output will sometimes exhibit CSI even though there was no SI in the scoring regime. Alternatively, we can say that a successful regime like Chellapilla and Fogel's40 has SI of -log2(1/720) = 9.49 bits, plus a few bits to allow for the fact that not all successful regimes perform as well as this one, as discussed above.
Having seen that very little if any SI was "inserted" through the choice of scoring regime, Dembski might choose to focus on other parameters, such as the population size. The beauty of Chellapilla and Fogel's algorithm, however, is that it has very few parameters and even those few could be varied considerably without adversely affecting the performance of the program. Nothing has been fine-tuned. Just as in the case of the scoring regime, the selection of those other parameters therefore involves little SI.
6.7 Counterexample: Mathematical Sequences
As discussed earlier, Dembski apparently considers that the 1126-bit SETI prime sequence exhibits 1126 bits of SI. But, if this is so, it follows that an n-bit sequence would exhibit n bits of SI. So a computer program which outputs this sequence can produce as much SI as we like, simply by letting the program run for long enough. The SI of the output could run into millions of bits and easily exceed the SI of the program, no matter how big that program is. Perhaps the task of generating primes is too intractable for this to be a practical possibility. In that case we can just pick a simpler sequence, such as the Fibonacci sequence. If we take a really simple sequence like the Champernowne sequence (p. 64), we can even program it in just a few machine code instructions and run it on a bare computer (with no operating system), so the total SI of the software is less than 500 bits, not even enough to constitute CSI.
I give the following justification for asserting that the SI of a program is no greater than the length of the program. Consider a given program of length N bits. By analogy to Dembski's METHINKS example (p. 166), I argue that I can take as my phase space the space of all programs of the same length as my given program. Then the probability of drawing any given program (i.e. sequence of bits) from a uniform distribution over this space is 1/2N, so the information of a particular program is -log2(1/2N) = N bits. The SI exhibited by the program may be less than this (if more than one program matches the same specification as the given program) but it cannot be more.
Since the SI of the program is finite (N bits) but the SI of the output sequence is unlimited, the program can generate an unlimited amount of SI.
Let me address all the objections that Dembski might make to this argument:
"All the SI in the output was contained in the program." This means that the program contains an unlimited amount of SI. I doubt that Dembski would like to take the position that a trivial program can contain an unlimited amount of SI.
"The SI of a mathematical sequence is limited to the length of the program that is needed to generate it." This is true of algorithmic information (Kolmogorov complexity),41 but not of Dembski's SI.
"The output of a deterministic process does not exhibit SI because it is not contingent, as required by the Explanatory Filter." But this would be making the evaluation of SI dependent on the type of causal process leading to the phenomenon, the very issue that is in question. If the SETI sequence exhibits CSI when it is received from outer space, why should the same sequence not exhibit CSI when it is produced by a computer? And for all we know, the SETI sequence might also have been generated by a deterministic computer program (programmed by ETs). In any case, we can make our computer program non-deterministic if required, e.g. by starting the prime sequence from a randomly selected prime.
The problem for Dembski is that highly patterned phenomena are tightly specified, giving them low probability and therefore high SI. Unlike algorithmic information (Kolmogorov complexity), which is a measure of incompressibility, SI correlates with compressibility. Highly compressible sequences like the SETI sequence exhibit high SI. Dembski seems quite happy with this fact:
It is CSI that within the Chaitin-Kolmogorov-Solomonoff theory of algorithmic information identifies the highly compressible, nonrandom strings of digits... [p. 144]
So Dembski's information (SI) tends to vary inversely with algorithmic information. A highly compressible sequence can be high in SI but low in algorithmic information. Dembski leads us to believe that his CSI is equivalent to the term specified complexity as used by other authors, giving the following quotation from Paul Davies' book The Fifth Miracle no less than four times:
Living organisms are mysterious not for their complexity per se, but for their tightly specified complexity. [p. 180]
Yet, if we read The Fifth Miracle, we find that Davies uses complexity in the sense of algorithmic information (Kolmogorov complexity), and not Dembski's probability-under-a-uniform-distribution sense. Davies also calls his measure specific randomness, whereas Dembski identifies CSI, in the quote above, with nonrandom strings.42
In a similar vein, Dembski quotes Leslie Orgel:
Living organisms are distinguished by their specified complexity. Crystals such as granite fail to qualify as living because they lack complexity; mixtures of random polymers fail to qualify because they lack specificity. [p. 229n5]
But, by Dembski's definition, crystals have high complexity, because the probability of obtaining a crystal shape by purely random combination of molecules is very small. Like Davies, Orgel defines complexity in terms of "the minimum number of instructions needed to specify the structure".43
So, contrary to Dembski's implications, his concept of specified complexity is quite different from that of Davies and Orgel.44
6.8 Dembski's Mathematical Justification
Dembski claims to have provided a mathematical justification for his LCI. Since we've just seen that counterexamples to the LCI can easily be found, there must be something wrong with the mathematical justification. In fact, the errors aren't too hard see.
The first 4 pages of Dembski's justification (pp. 151-155) are concerned with showing that the LCI is true for deterministic processes. The error in this argument can be seen most clearly by starting from the following equation (p. 152):
I(A&B) = I(A) + I(B|A).
Since B (the result of a deterministic process) is entirely determined by A (the antecedent conditions), argues Dembski, I(B|A) = 0, and therefore I(A&B) = I(A). Thus, no new information has been produced by the process. (I've simplified Dembski's notation a little.)
The equation above was derived from the following basic probability equation, simply by transforming both sides of the equation by the trivial transformation I(E) = -log2P(E):
P(A&B) = P(A) × P(B|A)
which Dembski states in the following form (pp. 128-129):
P(B|A) = P(A&B) / P(A).
So Dembski's result is just another way of saying that the result of a deterministic process occurs with probability 1. But this tells us nothing about the specified information exhibited by the result, since that is based on a uniform probability distribution, regardless of the true probability.
For the sake of a concrete example, let's consider one of the mathematical sequences above, say the 1126-bit SETI prime sequence. Then A is the program producing the sequence and B is the sequence itself. Then it's true that P(B|A) (the probability of B given A) is equal to 1, since A always leads to B. Therefore, applying the transformation I(E) = -log2P(E), we arrive at I(B|A) = 0. So far, so good. However, I(B|A) here is not Dembski's specified information, SI. I assume that the events in question are specified, so the problem has nothing to do with specification. The problem is that I(B|A) is just P(B|A) transformed, and P(B|A) is the true conditional probability of the event, which in this case is 1. SI, on the other hand, is based on the assumption of a uniform probability distribution, regardless of the true probability of the event. In the SETI case, the SI exhibited by B is given by
SI = -log2(P(B|U)) = -log2(2-1126) = 1126 bits
where U indicates a uniform probability distribution over the space of all possible 1126-bit sequences.
In short, Dembski is equivocating between two different meanings of information.
So deterministic processes can generate CSI. However, Dembski could have avoided this problem by adopting a sensible measure of information, such as Davies' specified Kolmogorov complexity. With that measure, it would be true that deterministic processes cannot generate information, since the output of a deterministic program by definition has the same or less Kolmogorov complexity than the program. In order to address Dembski's arguments regarding stochastic processes, I will pretend, for the remainder of this section, that SI cannot be generated by deterministic processes.
The next stage in Dembski's justification is to argue that purely random processes cannot generate CSI (pp. 155-157). I will happily agree that this is so, given the following elaboration of what I mean by it: we consider it effectively impossible that a highly specified phenomenon (such as a living organism) could be drawn from a uniform probability distribution over the space of all possible combinations of the phenomenon's component parts (if we take sufficiently simple parts). The probability is just too low. This would be what Richard Dawkins calls single-step selection.45 However, as Dembski points out, purely random processes can produce smaller amounts of SI, short of CSI, since these correspond to events of larger probability. In other words, the LCI does not prohibit natural processes from producing SI.
But what about cumulative selection (to borrow Dawkins' contrasting term)? Cumulative selection is a series of small steps through the phase space (the set of all possible configurations), based on trial and error, in which advantageous steps are retained and used as a basis for further development. What is Dembski's argument against the generation of CSI by cumulative selection? In addressing whether a stochastic process can generate CSI (pp. 157-158), Dembski breaks down the process into two stages: a pure chance stage followed by a deterministic stage. He argues that neither stage can produce CSI, and so the combined two-stage process cannot do so either. Strangely, Dembski doesn't mention the possibility of multiple iterations of chance and deterministic process. But that's exactly what cumulative selection (e.g. biological evolution) relies on. Each chance stage (random mutation) can produce a little SI, and natural selection can act to prevent the existing SI being lost, allowing it to accumulate over time in a ratchet-like process.
Dembski returns to this issue several pages later (pp. 165-166), when he claims that CSI is holistic, and so cannot be accumulated. But his argument in support of the claim utterly fails to address the issue. He points out that the sentence "METHINKS IT IS LIKE A WEASEL" exhibits more SI than the aggregate set of individual words {A, IS, IT, LIKE, WEASEL, METHINKS}, because the former consists of a specified sequence of words. Depending on what specifications we choose, that may be true. But it is irrelevant, as there is still no limit on the amount of SI that an aggregate can exhibit, given sufficient words. In any case, Dembski has given us no reason to think that natural causes are limited to producing randomly ordered aggregates.
The issue is not how much SI a structure can exhibit, but whether that SI can arise through natural processes, and Dembski gives no reason whatsoever to think that SI cannot be accumulated over multiple stages of cumulative selection. Perhaps Dembski would respond that the probability of the whole process achieving a specified result is the product of the probabilities of the individual stages, and so will still come out to be below the universal probability bound. But this would fail to recognize that at each stage there will be many attempts (many individuals in the population over many generations), so the probability of success will be far higher than if a single individual had to jump the hurdle of every stage in succession.
To sum up, Dembski has failed to show that natural processes cannot produce specified complexity or CSI, however defined. He has simply evaded the issue of cumulative selection.
Dembski makes the bold claim that his LCI can be considered a "fourth law of thermodynamics". Since I have shown the LCI to be baseless, I will not consider this additional claim.
Research! A mere excuse for idleness; it has never
achieved,
and will never achieve any results of the slightest
value.
Benjamin Jowett (1817-93), classical scholar
and Master of Balliol College, Oxford
Having previously denied the value of comparing hypotheses and relied on a purely eliminative approach to inferring to design, Dembski changes tack in his final chapter and attempts to make a positive case for his design hypothesis. Much of this is based on the premise that specified complexity is a marker of design, a premise which we have seen to be false. I will ignore those parts, and concentrate on the additional claims.
7.1 Outline of a Positive Research Program
The Intelligent Design movement has often been criticized for not conducting or even proposing any research, and Dembski tries to address this concern here (pp. 311-314). The first part of this "program" is the search for more cases of specified complexity, i.e. more biological systems for which there is allegedly no known natural explanation. Beyond this, all he presents is a list of questions, of which the following is typical:
Construction Problem--How was the designed object constructed? Given enough information about the causal history of an object, this question may admit an answer. [p. 313]46
No serious attempt is made to suggest how these questions might be answered. A list of questions does not constitute a research program!
Dembski's final question is: "Who or what is the designer?", but he quickly adds that this is not a question of science. How strange. I thought that Dembski, like other Intelligent Design proponents, was against the drawing of arbitrary lines between what can and cannot be included in science. Why should the identity of the designer be a forbidden topic?
The design hypothesis has often been criticized for being untestable. What exactly is meant by testability is unclear, but Dembski uses the term as a general heading under which to consider a number of more specific criteria.
Both supporters and opponents of Intelligent Design have an unfortunate tendency to assert that "Intelligent Design is/isn't falsifiable", without clarifying just what the hypothesis is that they are referring to. In fact, as we've already seen, Dembski's design hypothesis tells us no more than that a designer was involved somewhere in the causal chain of events leading to the bacterial flagellum (and possibly other biological systems). The design hypothesis says nothing at all about the identity, capabilities or aims of the designer; whether there were many designers or only one; or how and when the design was implemented.
The philosopher of science Karl Popper maintained that falsifiability is a necessary condition for a proposition to be considered a scientific hypothesis, and this principle has often been used as a demarcation criterion for separating science from pseudoscience. If there is no evidence that could possibly contradict a hypothesis, then the hypothesis can be maintained regardless of the evidence. The principle has been weakened by the observation (attributed to Duhem and Quine) that any hypothesis can be saved from falsification by abandoning an auxiliary hypothesis. For example, it is sometimes argued that the finding of a fossilized human skull in a Precambrian stratum would falsify the theory of evolution. But, even in the face of such an observation, the theory of evolution could be saved by supposing that there is some unknown means by which a fossil could sink through old strata. Nevertheless, we can think in terms of degrees of falsifiability. The theory of evolution is relatively falsifiable, because there are many hypothetical observations, like a skull in the Precambrian, which would cause significant consternation among scientists, requiring the re-evaluation of at least one well-supported scientific hypothesis.
On the other hand, there is no potential observation which could cause any such problem for proponents of the design hypothesis, since any observation whatsoever is consistent with that hypothesis, with or without any auxiliary hypotheses. Despite this, Dembski claims that the design hypothesis is falsifiable, while conceding that he has been "fast and loose" in his use of the term (p. 357). His usage is indicated by the following passage:
If it could be shown that biological systems like the bacterial flagellum that are wonderfully complex, elegant and integrated could have been formed by a gradual Darwinian process (which by definition is non-telic), then intelligent design would be falsified on the general grounds that one does not invoke intelligent causes when purely natural causes will do. In that case Occam's razor finishes off intelligent design nicely. [p.357]
All Dembski is saying here is that the design hypothesis has the potential to be replaced by a better one. But that's true of any hypothesis, so the point is quite uninteresting. This is certainly not what Popper meant by falsifiability.
It is refreshing that, by his invocation of Occam's razor, Dembski seems to have recognized that the hypothesis of natural evolution is more parsimonious than the design hypothesis. One is bound to ask, then, why he thinks a hypothesis (design) which is entirely lacking in detail should be preferred to a more parsimonious hypothesis (natural evolution) with limited detail. Clearly design hypotheses have a very privileged status in Dembski's system.
Predictive power (or predictability as Dembski calls it) is closely related to falsifiability (in Popper's sense), since a hypothesis is falsified by making an observation which contradicts a prediction of the hypothesis. For a hypothesis to make predictions, it must be able to distinguish between those observations which are possible under the hypothesis and those which are not, or else those which are more likely than others. The design hypothesis fails absolutely in this. With no knowledge of the designer's abilities and aims, all conceivable possibilities appear equally likely.
In an earlier article, Dembski acknowledged the lack of predictive power of the design hypothesis: "Yes, intelligent design concedes predictability."47 In No Free Lunch he backs away from this concession, offering two examples of predictions made by the design hypothesis, but neither of these stands up to scrutiny.
First he tells us that "Intelligent design offers us one obvious prediction, namely, that nature should be chock-full of specified complexity and therefore should contain numerous pointers to design" (p. 362). Not at all. The design hypothesis tells us nothing about how many structures were designed, and Dembski himself previously told us (p. 24) that design does not necessarily leave any detectable traces. He even writes:
Please note that I am not offering a theory about the frequency or intermittency with which an unembodied designer imparts information into the world. I would not be surprised if most of the information imparted by such a designer will elude us, not conforming to any patterns that might enable us to detect this designer... [pp. 346-347]
Next he appeals to patterns that have been recognized in the evolution of human technology, arguing that the design hypothesis predicts we should see such patterns in biological evolution too (p. 362). But why should that be? Is Dembski now telling us that his unembodied designer is constrained to follow similar patterns of development to human designers? If so, then that is an addition to the design hypothesis which does indeed have some predictive implications. But it cuts both ways. If we find patterns in evolution which are not typical of human technological development, that will count as evidence against the design hypothesis. And we do find such patterns. For example, we see that biological evolutionary changes occur in piecemeal fashion, with systems being adapted to completely new functions, where a human designer would redesign the system from the ground up. Often this leads to suboptimal systems such as the inverted mammalian retina, with its blind spot, which could be improved by a simple change, easily made by a human engineer but possibly inaccessible to natural evolution.48 So Dembski has a choice here: no predictive power or predictive failure. Which will it be?
Having failed to establish any predictive power for his own hypothesis, he tries to turn the tables on evolutionary theory, pointing out that evolutionary theory does not predict such facts as the existence of particular species (p. 361). This is true, as such facts are the result of unpredictable historical contingencies. But evolutionary theory certainly does make many predictions all the same.49 For example, evolutionary theory predicts that there will be a high degree of congruence between phylogenetic trees derived from morphological studies and from independent molecular studies. This prediction has been confirmed, and continues to be confirmed as more species are tested.50
Proponents of Intelligent Design will sometimes argue that much of the predictive power of evolutionary theory can be assimilated by Intelligent Design. For example, those who accept the common ancestry of species may argue that the congruence of phylogenetic trees is a prediction of common ancestry, regardless of whether the descent from a common ancestor was controlled by a designer or not. Dembski does not appear to make such an argument, and indeed is quite ambivalent about common ancestry (pp. 314-316). In any case, the introduction of a designer into the evolutionary process weakens the predictions from common ancestry, since it forces us to allow, for example, for the designer suddenly introducing entirely new genetic material. The only way to fully preserve the predictive power of evolutionary theory while introducing a designer is to hypothesize that the designer perfectly mimics the empirical effects of natural evolution. Such a hypothesis is entirely superfluous from a scientific point of view.
The term explanatory power is widely used but difficult to define. I will not attempt a definition, but will note that, in part, it is another face of predictive power, referring to the ability to "retrodict" past observations. In this sense, the design hypothesis is as totally lacking in explanatory power as in predictive power.
Dembski claims that there are "things that might occur in biology for which a design-theoretic framework could give a better, more accurate account than a purely Darwinian and therefore nonteleological framework" (p. 363). To support this claim, he gives just one example:
To see this, suppose that I were a supergenius molecular biologist and that I invented some hitherto unknown molecular machine, far more complicated and marvelous than the bacterial flagellum. Suppose further I inserted this machine into a bacterium, set this genetically modified organism free, allowed it to reproduce in the wild, and destroyed all evidence of my having created the molecular machine. Suppose, for instance, the machine is a stinger that injects other bacteria and explodes them by rapidly pumping them up with some gas (I am not familiar with any such molecular machine in the wild), thereby allowing bacteria endowed with my invention to consume their unfortunate prey.
Now let us ask the question, If a Darwinist came upon this bacterium with the novel molecular machine in the wild, would that machine be attributed to design or to natural selection?" [p. 364]
Dembski tells us that "intelligent design, by focusing on the stinger's specified complexity, would confirm the stinger's design whereas Darwinism never could" (p. 364). What nonsense! There is no reason why a Darwinist (i.e. mainstream scientist) should not consider the possibility of human design, just as he or she might suspect genetic engineering of an unusual new strain of tomato, or selective breeding of a dog. In the case of Dembski's stinger, we would consider such factors as whether the device was within the reach of current technology, what motive someone might have for creating it, whether the device had the appearance of an evolved structure, whether there were any known similar organisms from which this one might have evolved, etc.
In any case, this has nothing to do with whether there is any explanatory power to the hypothesis that an unknown being designed the bacterial flagellum. In Dembski's example we would be considering a possible human designer with known (to some degree) capabilities and motivations.
So evolutionary theory wins out over the design hypothesis in terms of productivity as a research program, falsifiability, parsimony, predictive power and (at least by the definition considered above) explanatory power.
Dembski makes no attempt to conceal the fact that the designer he has in mind is an unembodied one. Why, he asks, are scientists willing to consider design involving alien beings (as in SETI) but not unembodied designers? He answers the question himself:
At least with extraterrestrial intelligences we can guess what might have happened. But we do not have any experience with unembodied designers, and that is clearly what we are dealing with when it comes to design in biology. [p. 359]
This is exactly the point. In the case of SETI, we can consider the possibility that aliens evolved naturally, developed the technology to send a radio signal across interstellar space, and decided it was worth trying to communicate with us. There are enormous uncertainties involved, but we can make an informed guess about the relative plausibility of such a hypothesis as compared with the hypothesis that an extraterrestrial radio signal is of natural origin.
An unembodied designer, on the other hand, is quite another matter. Dembski defines an unembodied designer as "an intelligence whose mode of operation cannot be confined to a physical entity located within spacetime" (pp. 333-334). We have no idea how such a being could exist or even what it means for such a being to exist. I for one do not rule unembodied beings out of science as a matter of principle, but it would require some very significant new developments in science before such a hypothesis could be seriously entertained. In the meantime, unembodied designers are a highly unparsimonious explanation.
Not only does Dembski fail to explain the nature of his unembodied designer, he even tries to rule questions about its origin out of bounds:
The who-designed-the-designer question invites a regress that is readily declined. The reason this regress can be declined is because such a regress arises whenever scientists introduce a novel theoretical entity. For instance, when Ludwig Boltzman introduced his kinetic theory of heat back in the late 1800s and invoked the motion of unobservable particles (what we now call atoms and molecules) to explain heat, one might just as well have argued that such unobservable particles do not explain anything because they themselves need to be explained. [p. 354]
Of course it is true that scientific explanations often create new unanswered questions. But, in assessing the value of an explanation, these questions are not irrelevant. They must be balanced against the improvements in our understanding which the explanation provides. Invoking an unexplained being to explain the origin of other beings (ourselves) is little more than question-begging. The new question raised by the explanation is as problematic as the question which the explanation purports to answer. As Dawkins puts it (quoted by Dembski):
You have to say something like "God was always there", and if you allow yourself that kind of lazy way out, you might as well just say "DNA was always there", or "Life was always there", and be done with it. [p. 353]
Dembski's response is to attack "Dawkins's reductionist view of science" (p. 353). But this is not reductionism. It is the principle that scientific explanations should actually explain things, and not just beg the question!
Jay Richards, another proponent of Intelligent Design, also weighs in with some empty rhetoric: "If a detective explains a death as the result of a murder by, say, Jeffrey Dahmer, no one says, 'OK, then who made Jeffrey Dahmer?'" (p. 355). Since we know perfectly well that Jeffrey Dahmer existed, there is obviously no reason for us to ask that question. If, on the other hand, the detective announced that the victim was killed by an android (a type of artificial person described by many science fiction novels), and if we had no independent evidence of the existence of androids, we would certainly demand an explanation of how such a being could have come into existence.
One thing that Dembski is willing to say about his proposed unembodied designer is that it probably intervenes in the world through manipulation of non-deterministic quantum events:
Thermodynamic limitations do apply if we are dealing with embodied designers who need to output energy to transmit information. But unembodied designers who co-opt random processes and induce them to exhibit specified complexity are not required to expend any energy. For them the problem of "moving the particles" simply does not arise. Indeed, they are utterly free from the charge of counterfactual substitution, in which natural laws dictate that particles would have to move one way but ended up moving another because an unembodied designer intervened. Indeterminism means that an unembodied designer can substantively affect the structure of the physical world by imparting information without imparting energy. [p. 341]
For now, however, quantum theory is probably the best place to locate indeterminism. [p. 336]
No suggestion is made as to how the desired quantum events might be "induced".
Empty vessels make the most noise.
Traditional proverb
It is usual for academics, particularly those in technical fields, to submit their work to review by their peers, their fellow academics with expertise in the relevant fields. This usually takes the form of submission to specialist journals in which papers must undergo a process of peer review before publication. In the long run what matters is whether an idea is accepted by the experts in the relevant field, but the process of peer review provides a first sifting to weed out half-baked ideas. Academics also present their work to their peers at academic conferences. However, Dembski, like other Intelligent Design proponents, eschews these processes, preferring to sell his ideas directly to the public, and being careful to avoid review by the experts. He is quoted as having said:
I've just gotten kind of blasé about submitting things to journals where you often wait two years to get things into print. And I find I can actually get the turnaround faster by writing a book and getting the ideas expressed there. My books sell well. I get a royalty. And the material gets read more.51
Dembski claims to have provided a rational foundation for the Fisherian approach to statistics and to have discovered a new Law of Conservation of Information. If these claims were true, they would be of profound importance to statisticians and information theorists. He has even be hailed by one of his allies in the Discovery Institute as "the Isaac Newton of information theory".52 Yet his work on these subjects has not appeared in any journal of statistics or information theory, and, as far as I can determine, not one professional statistician or information theorist has approved of this work. Had any done so, I am sure we would have heard about it from Dembski himself, since he makes a habit of using informal references as a substitute for peer review:
Mathematicians and statisticians have been far more receptive [than philosophers] to my codification of design inferences. Take, for instance, the positive notice of The Design Inference in the May 1999 issue of American Mathematical Monthly as well as mathematician Keith Devlin's appreciative remarks about my work in his July/August 2000 article for The Sciences titled "Snake Eyes in the Garden of Eden": "Dembski's theory has made an important contribution to the understanding of randomness--if only by highlighting how hard it can be to differentiate the fingerprints of design from the whorls of chance."53 [p. 372n2]
Keith Devlin is a respected and widely published mathematician, but he is not a statistician. His article was of a general nature in a popular magazine, not a scholarly journal, and did not address the details of Dembski's work. The content of the article overall was rather more negative towards Dembski's work than the concluding remark suggests.54 The "positive notice" in the American Mathematical Monthly reads as follows, in its entirety:
Probability, S, P, L. The Design Inference: Eliminating Chance Through Small Probabilities. William A. Dembski. Stud. in Prob., Induction, & Decision Theory. Cambridge Univ Pr, 1998, xvii + 243 pp, $54.95. [ISBN 0-521-62387-1] Not a text but a philosophical tract about when one can infer design behind events of very small probability. Thought provoking, fun to read, full of interesting examples. SN55
The fact that Dembski has to resort to such barely favourable references for support indicates the complete lack of acceptance of his work by the experts in the relevant technical fields.
We are told (by Dembski and the publisher) that The Design Inference did undergo a review process, though no details of that process are available. It is interesting to note, however, that The Design Inference originally constituted Dembski's thesis for his doctorate in philosophy, and that his doctoral supervisors were philosophers, not statisticians. The publisher (Cambridge University Press) catalogues the book under "Philosophy of Science". One suspects that the reviewers who considered the book on behalf of the publisher were philosophers who may not have had the necessary statistical background to see through Dembski's obfuscatory mathematics. In any case, much of the material in No Free Lunch, including the application of Dembski's methods to biology, did not appear in The Design Inference, and so has received no review at all.
Better is the end of a thing than its
beginning...
Ecclesiastes 7:8.
No Free Lunch is characterized by muddled thinking, fallacious arguments, errors, equivocation and misleading use of technical jargon. Once these are cleared up, the following conclusions become apparent:
The chance-elimination method is nothing but a god-of-the-gaps-argument. It merely tells us to infer design when we have rejected all the non-design hypotheses we can think of.
In applying the chance-elimination method to a biochemical system (the bacterial flagellum), Dembski has failed to consider evolutionary explanations involving change of function. Instead, he merely considers and rejects an absurd hypothesis based on purely random combination of parts--the tornado in a junkyard scenario.
The No Free Lunch theorems have no applicability to biological evolution.
The argument from alleged fine-tuning of fitness functions turns out to be just a trivial variation on the well-known argument from cosmological and terrestrial fine-tuning.
Dembski's idiosyncratic concepts of complexity and information are misleading, and his so-called Law of Conservation of Information is fatally flawed.
Specified complexity (CSI) is not a marker of intelligent design. If specified complexity is determined according to the uniform-probability interpretation, then natural processes are perfectly capable of generating it. If it is determined by the chance-elimination method, then specified complexity is just a disguise for the god-of-the-gaps argument.
Dembski's claims about statistics, information theory, evolutionary algorithms and thermodynamics have not undergone peer review and have not been accepted by the experts in those fields.
In short, No Free Lunch is completely worthless, except as a work of pseudoscientific rhetoric aimed at a mathematically unsophisticated audience which may mistake its mathematical mumbo jumbo for genuine erudition. However, since I have been urged to find something positive to write about it, I am pleased to be able to report that the book has an excellent index.
I am grateful for the assistance of Wesley Elsberry, Jeffrey Shallit, Erik Tellgren and others who have shared their ideas with me.
Dembski's statistical method for rejecting individual chance hypotheses is derived from the approach to statistical inference developed by the statistician and geneticist R. A. Fisher. Although in widespread use due to its intuitive appeal, this approach is increasingly rejected by statisticians, including those who advocate the Neyman-Pearson, Bayesian and likelihood approaches. It is not my intention here to try to settle this long-standing controversy in statistical theory, but to point out problems with those of Dembski's claims which are additional to the standard account of Fisher's approach.
Dembski ambitiously claims to have provided a firm rational foundation for Fisher's statistical approach--something which has always been absent in the past--enabling him to extend the approach to a wider class of rejection regions (specifications) than those allowed by Fisher himself, and to provide non-arbitrary small probability bounds (pp. 45-47). Most of this appendix will be concerned with showing the major problems inherent in Dembski's methods for establishing specifications and probability bounds. I will finish by returning to the subject of whether he has provided a rational foundation for Fisher's approach.
He also tries to use his extension of Fisher's approach to justify his eliminative method of inferring design. But this is a red herring. As shown in section 3.3 above, Dembski's chance-elimination method simply involves applying his statistical method to each available chance hypothesis in turn, and inferring design if the statistical method rejects all the chance hypotheses we can think of. Therefore, in this appendix, I will have nothing further to say about "sweeping the field of chance hypotheses", as Dembski puts it (p. 67), but will simply consider Dembski's statistical method in terms of testing an individual chance hypothesis.
A.1 Specifications
An excellent comparison of the various approaches to statistics can be found in Howson and Urbach's Scientific Reasoning: The Bayesian Approach.56 This book is strongly recommended to any reader who wishes to understand the issue in detail. The clarity of exposition makes a refreshing antidote to Dembski's muddled thinking. Howson and Urbach make two major objections to Fisher's approach: the lack of a rational foundation, and the dependence of the outcome on the choice of test-statistic. Here is how they summarize the second objection:
Fisher's theory as so far expounded is logically inconsistent. The problem arises because there are always many random variables that may be defined on any given outcome space, and not all of them lead to the same conclusion when put to use as the test-statistic in a significance test. Hence, one test-statistic may instruct you to reject some hypothesis when another tells you not to."57
This problem is seen most clearly in the potential for tailoring the choice of test-statistic to the particular outcome observed, guaranteeing that the rejection region will be narrowly focused on that outcome and that the calculated probability will be small. For example, in the Caputo case, we might choose as our test-statistic the indicator function 1E which maps the observed outcome E to a value of 1 and all other outcomes to a value of 0. This leads to a rejection region consisting of E alone, with the result that P(R|H) = P(E|H) = (1/2)41. Dembski warns us about tailoring:
What needs to be precluded, then, is the tailoring of f [the test-statistic] to E. Alternatively, f needs to be independent (in some appropriate sense) of the sample E. [p. 54]
Fisher did not allow unlimited tailoring of the test-statistic to the observed outcome E, but no clear boundary was ever drawn between what was and was not allowed. He would have allowed the test-statistic used by Dembski in the Caputo case (the number of Ds in a sequence), but he would not have allowed the test-statistic just discussed (the indicator function 1E). Neither, I think, would he have allowed the test-statistic chosen by Dembski in the Champernowne case, which is discussed below.
In an attempt to resolve this problem, while widening the range of permissible test-statistics, Dembski introduces some rules which purportedly constrain us to choose only appropriate test-statistics, and hence only appropriate rejection regions. Patterns describing the appropriate (or detachable) rejection regions are called specifications while those describing inappropriate ones are called fabrications:
Patterns thus divide into two types, those that in the presence of complexity [low probability] warrant a design inference and those that despite the presence of complexity do not warrant a design inference. The first type of pattern I call a specification, the second a fabrication. Specifications are the non-ad hoc patterns that can legitimately be used to eliminate chance and warrant a design inference. In contrast, fabrications are the ad hoc patterns that cannot legitimately be used to warrant a design inference. As we shall see in chapter 2, the distinction between specifications and fabrications can be made with full statistical rigor. [p. 12]
The hollowness of this claim to rigour will soon become apparent.
Let us start by noting that Dembski uses the term rejection function instead of test-statistic. In fact, he uses the term ambiguously to refer both to the test-statistic itself and to its probability density function (or its probability function in the case of a discrete random variable) (pp. 50, 62). I will use the term in the former sense, i.e. as a synonym for test-statistic.
To illustrate the role of the rejection function in determining the specification, I will consider another one of Dembski's examples. A sequence of 100 heads and tails is generated, allegedly by tossing a fair coin 100 times, and a particular pattern is observed in the sequence (pp. 15-18). The first 50 results in the sequence (labelled E) are as follows:
E:THTTTHHTHHTTTTTHTHTTHHHTTHTHHHTHHHTTTTTTTHTTHTTTHH...
On converting to binary digits, the sequence is seen to consist of all the 1-digit binary numbers in ascending order, followed by the 2-digit binary numbers, and so on:
D: 0|1|00|01|10|11|000|001|010|011|100|101|110|111|0000|0001|0010|0011|...
This sequence is known as the Champernowne sequence (p. 64), and will be called D.
The first step in choosing a specification is to select what Dembski calls background knowledge (K). This is, broadly speaking, any subset of all the knowledge that was available to us before observing the event in question. In this case, Dembski selects "our knowledge of binary arithmetic and lexicographic orderings". From this he derives a rejection function, in this case the indicator function 1D, which maps outcome D to the value 1 and all other outcomes to the value 0. Finally, from this rejection function Dembski obtains the specification consisting of the single outcome E.
So there are three steps to reaching a specification: select background knowledge; from background knowledge to rejection function; from rejection function to specification. The last of these is not entirely unproblematic, but I will not consider it here. I will just consider the problems of the first two steps.
First, we have enormous latitude in our choice of K. Dembski imposes what he calls a conditional independence criterion, the effect of which is to prevent us including any information which directly tells us anything about the outcome. However, it does not prevent us from including information the choice of which tells us something about the outcome. This means that, when we choose K after observing the outcome, our choice of specification will not be statistically independent of the outcome, and this is indeed the case in Dembski's own examples.
Consider the example above. Dembski states that K is conditionally independent (i.e. statistically independent given the chance hypothesis in question) of the outcome because our knowledge of binary arithmetic and lexicographic orderings does not tell us anything about whether the sequence E has occurred. Perhaps so. But our decision to select "our knowledge of binary arithmetic and lexicographic orderings" as our background information was very much dependent on the outcome. If, for example, we had observed a sequence of prime numbers in the coin tosses, we would have selected "our knowledge of prime numbers and lexicographic orderings" as our background knowledge. Thus, the rejection function derived from this background knowledge is not statistically independent of the outcome, and neither is the resulting specification.
Indeed, Dembski does not claim that his specifications are statistically independent of the outcome, only that they are independent in "in a certain well-defined sense" (p. 15). But this is a peculiar sense which is quite different from both our everyday sense of the word and the technical sense used by statisticians. Nor is it even well-defined, as we see below.
Second, Dembski does not tell us how to derive the rejection function from our chosen background knowledge. He tells us we must select background knowledge "that explicitly and univocally identifies the rejection function f" (p. 72), but this is clearly not the case in the two examples which he gives us.
Consider again the example above. The selected background knowledge ("our knowledge of binary arithmetic and lexicographic orderings") clearly does not univocally identify the rejection function 1D, which is based on the Champernowne sequence (D). There are many other patterns involving binary arithmetic and lexicographic orderings on which we could have based our rejection function, e.g. a simple sequence of consecutive binary numbers:
0|1|10|11|100|101|110|111|1000|1001|1010|1011|1100|1101|1110|1111|...
Dembski's failure to follow his own rule is indicative of the more general problem. The concept of "deriving" a rejection function or pattern from our knowledge of binary arithmetic and lexicographic orderings (or any other set of knowledge) is not well-defined. This vagueness leaves us with further latitude to tailor the rejection function to the observed outcome.
In case Dembski responds that he could have selected "our knowledge of the Champernowne sequence" as his background knowledge instead of "our knowledge of binary arithmetic and lexicographic orderings", let me point out that this still would not univocally identify a rejection function. We can invent any number of variants on the Champernowne sequence. If we had observed a Champernowne sequence preceded by 5 superfluous digits, Dembski could have chosen the rejection function which counts the number of digits preceding the Champernowne sequence (or 100 if there is no Champernowne sequence). This would lead to the specification "Champernowne sequence preceded by 5 or fewer superfluous digits". If we had observed a variant Champernowne sequence which excludes all binary numbers with an even numbers of digits, Dembski could have chosen some other rejection function tailored to this particular variant. And so on.
The two problems just described combine to allow a high degree of tailoring of the rejection function (and hence the specification). To see the sort of extremes to which tailoring could potentially be taken, consider the following examples.
Let us suppose that the judge in the Caputo trial was a proponent of Dembski's method. Instead of adopting the specification "40 or more Ds", he might have adopted the narrower specification "22 Ds, then an R, then 18 more Ds" (based on the single observed outcome E), justifying this choice with the following argument: "While I was on my school's football team, we lost the first 22 matches we played, won 1, and then lost the remaining 18. So 22-1-18 is a pre-existing pattern, and I select it as my background knowledge K. From this, I derive the rejection function 1E, and hence the specification '22 Ds, then an R, then 18 more Ds'."
It might be argued that the judge's football record is irrelevant to the Caputo case. But no such relevancy criterion is currently included in Dembski's method, and, if background knowledge were to be excluded on the grounds of relevancy, this would be a highly subjective criterion. If we observe a suspiciously regular pattern with no knowledge of its cause, and want to test whether it arose from a certain probability distribution, how can we decide whether any given piece of background knowledge is relevant to it?
Now suppose that the judge had not seen such a sequence before. He might still argue for the specification "22 Ds, then an R, then 18 more Ds" on the following grounds: "I haven't seen the sequence 22-1-18 before, but I have seen the numbers 22, 1 and 18 separately. So I select them to form part of my background knowledge K, and then derive the rejection function from them." Since Dembski does not tell us how to derive a rejection function from a set of background knowledge, he has no grounds for declaring this derivation illegitimate.
I suspect Dembski's failure to notice problems like these is a result of the fact that all his examples are extremely simple ones. As soon as one looks at more complicated examples, the flaws in the method become much more apparent. Here is a particularly problematic example, from another source:
Suppose ten dice are rolled and we count the sum of them that comes up. It will be a number from 10 through 60. I want to maintain that whatever number it turns out to be, that number will not only be unlikely to have come up but it will have at least one unique and interesting property, not possessed by any of the other fifty numbers. For example, if it is, say, 25, then that number would be the only perfect square which is itself the sum of two squares (9 & 16) and is also the only odd number that is the square of its last digit. The number 27 is the only perfect cube of all of them. The number 28 is the only one that is the sum of all its divisors smaller than itself (1, 2, 4, 7, 14). The number 30 is the largest number X such that all numbers smaller than X with no divisor in common with X (other than 1) are themselves prime numbers. The number 32 is the smallest power of 2 such that the next number after it is not a prime (since the next number after 16 is a prime). The number 36 is the only one that is the product of two squares (4 & 9) and is the only even number that is the square of its last digit. The number 11 is the smallest palindromic number and 55 is the largest. The number 59 is the largest prime number. And 60 is that number which can be factored in more ways than any smaller number. I claim that every number from 10 through 60 has at least one unique and interesting property, especially if non-mathematical properties are included (such as 26 = the number of letters in the English alphabet; 29 = the number of days during February in a leap year; 31 = the most points that can be scored in a hand of cribbage, and so on). In light of this fact, no matter what number comes up as the sum of the ten dice, we could say, "How amazing: not only is that number highly unlikely to have come up but it is the only number such that ..." and proceed to specify the interesting property or properties uniquely possessed by that number. Then we could ask: "What is the explanation for the fact that that number came up rather than some other number?" The correct answer is that it is just a coincidence (or brute fact) that that number came up, and whatever number had come up, it would have been unlikely to have done so and, further, there would have been some interesting property or properties possessed only by that number.58
I suggest that, in this example, no matter what outcome we observed, Dembski's approach could be used to justify a rejection region consisting of just the specific observed outcome.
To sum up this section: we now see that Dembski's method for distinguishing between specifications and fabrications is far from exhibiting the "full statistical rigor" that he claimed. On the contrary, the distinction between specifications and fabrications is highly arbitrary, allowing a high degree of tailoring of the specification to the observed outcome.
But does this matter? In addition to the concept of specifications, Dembski has also introduced the concept of specificational resources. Although he doesn't state this explicitly, the purpose of specificational resources is to compensate for the tailoring of specifications.
Having chosen a specification and calculated the probability of any outcome matching that specification, Dembski's method requires us to compare this probability with a probability bound α, and to reject the chance hypothesis H if P(R|H) < α. In order to establish a value for α, Dembski introduces the concept of probabilistic resources:
Probabilistic resources comprise the relevant ways an event can occur (replicational resources) and be specified (specificational resources). The important question therefore is not What is the probability of the event in question? but rather What does its probability become after all the relevant probabilistic resources have been factored in? [p. 21]
The number of probabilistic resources is the product of the number of replicational resources (ReplRes) and the number of specificational resources (SpecRes). α is then determined by dividing the number 1/2 by this product:
α = ½ ÷ (ReplRes × SpecRes).
However, as the last quote suggests, Dembski often writes as if the probabilistic resources are factored into P(R|H) (by multiplication) rather than into α (by division). This makes no difference to the truth value of the inequality P(R|H) < α, of course, but it seems natural to think in terms of multiplying P(R|H) by SpecRes as a compensation for the excessive lowering of this probability which results from narrowly tailoring the specification to the observed outcome.
SpecRes is the number of potential specifications which we might have chosen before we were aware of the outcome. However, we only count potential specifications which have lower (or equal) probability and "complexity" than our chosen specification (corresponding to our rejection region R) and we ignore specifications which are subsets of other specifications we are counting (p. 77). I will refer to specifications which meet these criteria as relevant specifications, so that SpecRes is the number of relevant specifications.
I referred above to the "complexity" of a specification. It is important to note that this is not the same type of complexity that Dembski defines elsewhere as a monotonic function of probability (-log2P). According to Dembski, he is now referring to "a complexity measure φ that characterizes the complexity of patterns relative to S's [a subject's] background knowledge and abilities as a cognizer to perceive and generate patterns" (p. 76). The vagueness of this concept is not helped by a note, in which Dembski gives no less than three interpretations (p. 118n29):
"Computational complexity." This is a measure of the amount of computational resources (such as computer time and memory) needed to solve a problem (p. 140).
"The degree of compressibility of a specification as measured within algorithmic information theory." This is Kolmogorov complexity (Dembski clearly means in-compressibility),41 and is an attribute of an object, such as a sequence of characters, not an attribute of a problem, so is not commensurate with computational complexity.
A subject's "disposition to output a given specification." No idea is given of how such a subjective concept might be measured.
In The Design Inference Dembski referred to this measure as the computational complexity or degree of difficulty associated with the problem of formulating a specification. But since he has never told us how specifications are formulated (i.e. how rejection functions are derived from background knowledge), this measure is not well-defined. Dembski's claim that "Such a measure is objectively given (relative to S)" (p. 76) is pure wishful thinking. I'll refer to this measure as computational complexity.
In the Caputo case, Dembski lists the following potential specifications, after removing subsets (p. 81):
He suggests that there may be additional relevant specifications, but he thinks the number will not exceed a single digit, and takes the total number as 100 "to play it safe". No attempt is made to calculate the computational complexity of any specifications. It is just assumed that the computational complexity of specifications can be compared on some intuitive basis. The first of the above specifications is the one we chose for calculating P(R|H), and since the second exhibits an obvious symmetry with the first, it might be reasonable to take it as having the same computational complexity, although our background knowledge relating to Democrats is different from our knowledge relating to Republicans, and one wonders whether that should have an effect. Since Caputo would be expected to favour his own party, an outcome matching the first specification would appear more suspicious than one matching the second. How the computational complexity of the third specification is compared with that of the other two is a mystery. Finally, we are left to guess at how many more, unknown relevant specifications there may be. Whether 100 is a conservative overestimate is impossible to judge, given the vagueness of the criterion by which specifications are compared.
Dembski appears to suggest that the narrower the specification we choose for calculating P(R|H), the fewer relevant specifications there will be, and hence the smaller will be SpecRes. This supports the view that SpecRes compensates for the tailoring of the specification:
By factoring in all the relevant probabilistic resources, specification effectively precludes unbridled tailoring of events to rejection regions--each attempt to specify an event incurs a probabilistic cost that has to be counterbalanced by a probabilistic resource that takes that attempt into account. [p. 76]
While such a balancing mechanism is clearly welcome, Dembski makes no attempt to rationalize his particular criteria for calculating SpecRes. My own interpretation is that he is attempting to count all possible patterns which are as exceptional, in some sense, as the pattern noted in the observed outcome. Multiplying P(R|H) by SpecRes can then be interpreted as an attempt to estimate the probability of a larger rejection region which includes all the outcomes as exceptional as the observed one. However, given the number of highly subjective estimates that must be made and the lack of a rational foundation, it is not clear that this approach offers any advantage over simply asking the single question: "What proportion of potential outcomes would we consider as exceptional or more so than the observed one?"
A.3 Replicational Resources
Replicational resources are conceptually much simpler than specificational resources, but also suffer from the problem of arbitrariness. They are defined by Dembski as "the number of opportunities for a certain event to occur" (p. 19). For the Caputo case, he provides the following calculation of ReplRes:
The court is generous in handing out probabilistic resources. The court imagines that each state in the United States has c = 500 counties (an exaggeration), that each county has e = 5 elections per year (another exaggeration), that there were s = 100 states (we imagine rampant American imperialism doubling the number of states in the union), and that the present form of government endures y = 500 years (over double the current total). The product of c times e times s times y equals 125 million and signifies an upper bound on the total number of elections that might reasonably be expected to occur throughout U.S. history. These constitute the relevant replicational resources, which we denote by ReplRes, to account for Caputo giving Democrats the top ballot line 40 out of 41 times. [p. 81]
Although Dembski has been generous in estimating the values of his parameters (except, one hopes, for the life expectancy of U.S. democracy), the choice of parameters is arbitrary. In fact, there was only one opportunity for the specific observed event to occur. There were, of course, many opportunities for similar events to occur, but how do we decide how similar an event must be in order to qualify for inclusion in ReplRes? Why, for example, should we include county elections but not school board elections? Why elections in the U.S.A but not elections in other countries? Why not other events which involved 41 trials with just two possible outcomes, such as tossing 41 coins? Dembski's method forces us to draw an arbitrary line between events which we consider sufficiently similar to the observed one (such as elections in other states) and those which we consider insufficiently similar (such as elections in other countries).
On a point of detail, I note that Dembski counted the number of individual elections. But the event observed in the Caputo case involved 41 elections supervised by the same clerk. The number of times that one clerk draws the ballot order for a total of 41 U.S. county elections must be many times less than the total number of such elections.
From his estimates of SpecRes = 100 and ReplRes = 125 million, Dembski arrives at a figure of 1 in 25 billion for α, compared to a figure of 1 in 50 billion for P(R|H). He concludes that, since P(R|H) < α, "The New Jersey Supreme Court is warranted in inferring that E did not happen in accordance to the chance hypothesis H" (p. 82). With the inequality decided by a factor of only 2, this conclusion must be considered highly suspect, given the problems just described.
A.4 The Universal Probability Bound
Dembski recognizes that there is a degree of subjectivity involved in his method for establishing local probability bounds (at least as far as SpecRes is concerned), but claims that his universal probability bound avoids this problem:
Such a universal probability bound takes into account all the specificational resources that might ever be encountered in the known physical universe (interestingly, by exhausting the specificational resources of the universe, we also exhaust all the replicational resources that might ever arise). [p. 83]
As we saw earlier, the universal probability bound assumes that the maximum possible number of probabilistic resources is given by:
1080 × 1045 × 1025 = 10150
This is an estimate of the maximum number of elementary particle transitions that could possibly occur throughout the lifetime of the observable Universe. I think there are some grounds for questioning whether this actually represents the maximum possible number of events which could occur, since the same elementary event can be included in more than one composite event. I will not pursue this point, however, and will accept that this is the maximum possible number of replicational resources in the observable universe. It is far less clear, however, why this figure should be taken as the maximum possible number of specificational resources, let alone the maximum possible number of combined probabilistic resources (ReplRes × SpecRes).
Dembski's formal account of specificational resources (p. 77) is based on the number of potential specifications meeting certain criteria. There is no mention of any physical constraints on enumerating specifications. There is also no mention of any such constraint in the Caputo example. But, in order to set a universal upper limit on SpecRes, Dembski announces that we should only count the number of physical opportunities to formulate a specification. The nearest Dembski ever comes to providing a rationale for this constraint seems to be in the following passages:
That still leaves the problem, however, of a subject identifying numerous distinct items of background knowledge each of which is conditionally independent of E given H. Suppose each such item of background knowledge induces a rejection function that in turn induces a pair of rejection regions. Then each such rejection region is potentially capable of eliminating H. Hence by identifying sufficiently many items of such background knowledge, a subject can in principle run through one rejection region after another until hitting one that eliminates the chance hypothesis H. The worry, then, is that the Generic Chance Elimination Argument might eliminate any chance hypothesis whatsoever. [p. 74]
By factoring in all the relevant probabilistic resources, specification effectively precludes unbridled tailoring of events to rejection regions--each attempt to specify an event incurs a probabilistic cost that has to be counterbalanced by a probabilistic resource that takes that attempt into account. [p. 76]
Dembski seems to think that the only way the "subject" (the user of his method) might tailor the specification to the observed outcome is by running through all conceivable specifications until reaching one which is tightly tailored to the outcome. But this is a very peculiar conception of how the mind works. People do not identify patterns by running through every pattern they can think of and asking whether the observed pattern matches it. This simplistic idea of human thought processes seems particularly odd coming from Dembski, given his non-mechanistic view of intelligence (see section 2). Given the actual ability of people to detect patterns by rapid heuristic methods (as yet poorly understood), it is irrelevant how many individual specifications a human mind can elaborate, and Dembski's attempt to set a universal upper limit to SpecRes is doomed to failure.
Certainly, for many tests, 10-150 can be considered a very conservative bound. But it cannot be considered a universal bound, and the judgment of whether it is a suitable bound in a given case will remain a subjective one.
Incidentally, I could not help but laugh at Dembski's claim that the subjectivity of his method serves as confirmation of its soundness:
Subjective factors often do influence the setting of probabilistic resources, and the Generic Chance Elimination Argument faithfully reflects this fact (further confirmation that this argument schema provides a sound rational reconstruction of how we eliminate chance). [p. 83]
In fact, all methods of statistical inference involve subjective elements. The Bayesian and likelihood approaches make this quite explicit. It is, of course, an advantage to make clear the existence of those subjective elements, and Dembski does so in this instance but more often fails to do so, as we have seen. In any case, the idea that the existence of a subjective element indicates that his particular subjective method is a rational reconstruction of how we habitually think is absurd in the extreme.
A.5 The "Inflationary Fallacy" Fallacy
Some physicists have proposed that the universe we observe is just one in an ensemble of many universes. As Dembski points out, there are a number of different proposals of this sort, including the proposal that the observable universe is just one region within a vastly larger inflated universe, the many-worlds interpretation of quantum mechanics, and others. For brevity I will refer to all such proposals as "multiple universes". Dembski considers the possible relevance of multiple universes to the estimation of probabilistic resources, but dismisses the idea that they are relevant as "the inflationary fallacy" (pp. 86-87). He employs two arguments, neither of which stands up to scrutiny.
His first argument is that there is no "independent evidence" of multiple universes (pp. 90-92). Regardless of whether this is true--and I leave that question to physicists--it does not support Dembski's case. By adopting a purely eliminative method of inference, he has accepted the burden of rejecting all the natural hypotheses we can think of. The issue here is not whether the natural hypotheses have been shown to be true but whether Dembski can show them to be false. He is now trying to shift the burden of evidence which he voluntarily took upon himself.
Next, Dembski argues that unlimited probabilistic resources would allow bizarre possibilities such as Arthur Rubinstein being a world famous pianist yet knowing nothing at all about music, his music being nothing but an incredibly fortuitous random pounding on the piano keyboard. In fact, not all multiple universe hypotheses involve unlimited resources, but let us assume for the sake of argument that they do. Dembski himself gives the reason why such bizarre possibilities need not concern us:
Given unlimited probabilistic resources, there is only one way to rebut this anti-inductive skepticism, and that is to admit that while unlimited probabilistic resources allow bizarre possibilities like this, these possibilities are nonetheless highly improbable in the little patch of reality that we inhabit. Unlimited probabilistic resources make bizarre possibilities unavoidable on a grand scale. The problem is how to mitigate the craziness entailed by them, and the only way to do this once such bizarre possibilities are conceded is to render them improbable on a local scale. Thus in the case of Arthur Rubinstein, there are worlds where someone named Arthur Rubinstein is a world famous pianist and does not know the first thing about music. But it is vastly more probable that in worlds where someone named Arthur Rubinstein is a world famous pianist, that person is a consummate musician. What's more, induction tells us that ours is such a world. [p. 93]
Having for once made a cogent argument, but one which counters his own position, Dembski then spends the next two pages dancing around the issue, trying to undo his good work, but failing to come up with anything of substance.
In effect, if multiple universes exist, Dembski's universal probability bound of 10-150 becomes merely a local probability bound within the context of the ensemble of universes. For the vast majority of purposes, such as deciding whether Arthur Rubinstein could have played so well by pure chance, we need only consider this local probability bound, so the existence of multiple universes changes nothing. However, when considering the very special case of the origin of intelligent life, we must take into account the probabilistic resources of the full ensemble of universes. This is because of the well-known phenomenon of observational selection effect.59 Even if intelligent life occurs in only an infinitesimal proportion of a vast ensemble of universes, we should not consider ourselves lucky to find ourselves in one of those rare universes, since we could not find ourselves in any other. The same selection effect applies equally to any prerequisite for intelligent life, such as the origin of life itself. Dembski himself describes and accepts the relevance of this selection effect with regard to the number of planets on which life could potentially have originated,60 and exactly the same argument applies with regard to the number of universes in which life could potentially have originated.
It must be stressed that my refutation of Dembski's attempt to apply his design inference to biology does not rely on the existence of multiple universes. Dembski has failed to establish a small probability for the evolution of biological structures even relative to his own universal probability bound of 10-150.
A.6 A Rational Foundation?
Howson and Urbach comment as follows on the lack of a rational foundation for Fisher's approach (this passage is also quoted by Dembski in The Design Inference):
The force of a test of significance, Fisher then claimed, "is logically that of the simple disjunction: Either an exceptionally rare chance has occurred, or the theory of random distribution [i.e., the null hypothesis] is not true" (Fisher, 1956, p. 39). But in thus avoiding an unreasonably strong interpretation, Fisher plumped for one that is unhelpfully weak, for the significant or critical results in a test of significance are by definition improbable, relative to the null hypothesis. Inevitably, therefore, the occurrence of a significant result is either a 'rare chance' (an improbable event) or the null hypothesis is false, or both. And Fisher's claim amounts to nothing more than this necessary truth. It certainly does not allow one to infer the truth or falsity of any statistical hypothesis from a particular result. (Hacking, 1965, p. 81, has made the same point.)
Expositions of Fisherian significance tests typically vacillate over the nature of the conclusions that such tests entitle one to draw. For example, Cramér said that when a hypothesis has been rejected by such a procedure, "we consider the hypothesis is disproved" (1946, p. 334). He quickly pointed out, though, that "[t]his is, of course, by no means equivalent to a logical disproof". Cramér contended, however, that although a rejected theory could in fact be true, when the significance level is sufficiently small, "we feel practically justified in disregarding this possibility" (original italics altered). No doubt such feelings do often arise (though, as we shall see in Chapter 9, section c.3, there are exceptions to the rule); but Cramér offered no grounds for thinking that such feelings, when they occur, were generated by the type of reasoning employed in tests of significance, nor was he able to put those feelings onto any systematic or rational basis.61
Dembski believes he has accomplished what all other statisticians have failed to do--put Fisher's approach onto a firm rational foundation. He sums up his argument in No Free Lunch as follows:
The rationale here is that since factoring in all relevant probabilistic resources leaves us with an event of probability less than 1/2, the event is less probable than not, and consequently we should favor the opposite event, which is more probable than not and precludes it. [p. 79]
The argument is made at greater length in The Design Inference (pp. 193-198), but amounts to no more than this: if the saturated probability (i.e. the probability after factoring in all the probabilistic resources) of the event is less than 1/2, we should expect the event not to have occurred; but it did occur; this is a "probabilistic inconsistency"; to resolve the inconsistency, we should reject the chance hypothesis which conferred this probability on the event.
One might think that, if such a simple argument could provide a rational foundation for Fisher's approach, it would hardly have escaped the notice of the whole community of statisticians for so long!
In fact, Dembski's conclusion is a non sequitur. He gives no coherent reason why we should consider the occurrence of an unexpected event to be an "inconsistency". Unexpected events often do occur, and they do not necessarily lead us to revise the beliefs which rendered them unexpected.
Since Dembski is making a very ambitious claim, the onus is on him to make a sound argument in support of it, and he has signally failed to do so. Nevertheless, though not required to, I will give some counterexamples.
Consider this example: I toss a coin twice as a test of its fairness, specifying in advance that I will reject the hypothesis of fairness (that each toss has a 1/2 probability of resulting in a head) if I obtain two heads. To ensure that there will be only one trial of that coin, a newly minted coin is selected and the coin is destroyed after the trial. Since there can only be one trial, the number of replicational resources is 1. Since I have provided the specification in advance, there is only one possible specification and so the number of specificational resources is 1. Therefore the saturated probability of the event is 1/4. If I then proceed to obtain two heads, I should, apparently, infer that the coin was unfair. But I doubt that any reader of this article would draw that inference.
A similar example appears in The Design Inference (pp. 196-197), where Dembski insists that the subject must count as replicational resources all the coin tosses that he has made throughout his life. In fact, unlike my example, Dembski's subject did not stipulate in advance that the trial would be considered a test of the fairness of the coin or that there would only be one trial, so the examples are not equivalent. In any case, we could imagine, for the sake of argument, that I am replaced in my example with a person who has never tossed a coin before and swears never to do so again. Nevertheless, although I can see no grounds for him to do so, I suspect that Dembski will try to evade the force of this counterexample by claiming that we must count all the coin tosses ever made (or likely to be made) throughout the course of human existence. In case he should do so, I offer the following additional examples:
Consider a thought experiment in which a trial of the sort described above is the only time that coins are tossed throughout the whole existence of the human race.
Imagine the first trial of some radically new technological process, which sadly results in the destruction of the world. The only survivors are the inhabitants of a small lunar colony, who do not have the technology to repeat the trial and will not survive for long enough to obtain it. As it happens, one of the colonists had an interest in the new technology, and before the trial, specified the trial as a test of his hypothesis that the probability of global destruction was no more than 1/3. After the destruction, should he reject this hypothesis?
Consider the argument from cosmological fine-tuning, which attempts to infer design from the alleged minuscule probability of obtaining a life-enabling universe by random generation of the cosmological constants. If we were to accept Dembski's conclusion, then proponents of this argument would only need to show that the probability of a life-enabling universe was less than 1/2, rather than the vastly smaller probability which is actually claimed. The number of replicational resources in this case is only 1, since the argument is based on the assumption that there is only one universe. The number of specificational resources is also 1, given the specification "life-enabling universe", since we could not possibly have observed any other outcome. I doubt that the cosmological fine-tuning argument would enjoy its current popularity (or indeed any popularity at all) if the probability of a life-enabling universe had been shown to be 1/3.
A.7 Conclusion of the Appendix
Dembski's claim to have provided a rational foundation for Fisher's method of hypothesis testing is quite untrue, and his own version of the method suffers from much the same problems of arbitrariness as Fisher's. But does Dembski's method offer any advantages at all over Fisher's? It might be argued that, by trying to count the number of probabilistic resources, however subjectively, Dembski has at least broken down one subjective judgment (regarding the size of the probability bound) into a number of smaller, more manageable ones. Perhaps. But any such minor advantage must be offset against the fact that Dembski has allowed the user of the method much greater freedom to tailor the rejection region to the observed outcome, and against the confusion caused by Dembski's convoluted and equivocal exposition of what is really rather a trivial idea.
1. William Dembski, No Free Lunch: Why Specified Complexity Cannot be Purchased without Intelligence, Rowman & Littlefield, 2002.
2. I do not attempt to draw a hard line of demarcation between science and pseudoscience. By pseudoscience I mean egregiously bad science. See also: "pseudoscience", The Skeptic's Dictionary.
3. Richard Wein, "What's Wrong With The Design Inference", Metaviews online forum, October 2000.
4. William Dembski, "The Design Inference: Eliminating Chance Through Small Probabilities", Cambridge University Press, 1998.
5. William Dembski, "Intelligent Design Coming Clean", Metaviews online forum, November 2000.
6. My own view is that methodological naturalism is an ill-defined and arbitrary restriction which should be abandoned. The principle of "extraordinary claims require extraordinary evidence" is sufficient to prevent premature appeals to unembodied beings, but there is no reason to rule such beings out of science for all time regardless of what evidence might appear.
7. An outcome is an event which cannot be subdivided. It is also known as an elementary event. For example, in the Caputo case, each possible sequence of 41 Ds and Rs is considered a different outcome. The set of all such outcomes is known as the outcome space or sample space. (Dembski uses the term phase space.) Events such as "40 or more Ds" and "the 5th draw is a D" are known as composite events, because they consist of more than one outcome.
8. William Dembski, "The Explanatory Filter: A three-part filter for understanding how to separate and identify cause from intelligent design", 1996.
9. The term local probability bound occurs in Dembski's earlier work and not in No Free Lunch, but I find it convenient to use it here.
10. Dembski is rather vague about what inference should be drawn in the Caputo case. He considers only one chance hypothesis, namely the fair draw hypothesis H. Having rejected this hypothesis, Dembski does not clearly state that we should infer design, merely writing:
Step #8 [of the Generic Chance Elimination Argument] now follows immediately: The New Jersey Supreme Court is warranted in inferring that E did not happen according to the chance hypothesis H. [p. 82]
In stating that "Step #8 now follows immediately", he implies that we should infer specified complexity, and presumably an inference of design follows. But, as this is Dembski's only complete example of a design inference (other than the highly questionable case of the bacterial flagellum), a clear statement of the result might have been expected.
How sure are we that no other natural causes could have been operating? Dembski argues that H is "the only chance hypothesis that could have been operating to produce E... because Caputo himself was responsible for the ballot selections and claims to have used this chance process" (p. 80). He rules out the possibility that Caputo's randomization procedure was innocently flawed, on the grounds that Caputo drew capsules from a container, and that "urn models are among the most reliable randomization techniques available" (p. 56). Presumably this rejection of the possibility of a flawed urn procedure should be considered a proscriptive generalization. But what if Caputo was lying about the process he used, and actually used some other process which he thought to be fair but was not? It seems Dembski would still count this as "design".
So it appears that the inference of design in this case represents several possibilities: Caputo cheated, Caputo lied about his randomization method, or some other intelligent agent (perhaps unembodied) interfered in the process.
11. "Occam's Razor", Principia Cybernetica Web.
12. Dembski frequently claims that a certain event or phenomenon exhibits specified complexity, without having performed an explicit probability calculation. I take the liberty here of doing the same.
13. William Dembski, "The Intelligent Design Movement", Cosmic Pursuit, Spring 1998.
14. In support of their argument from the probability of purely random combination, Creationists often quote the astronomer Fred Hoyle: "The current scenario of the origin of life is about as likely as a tornado passing through a junkyard beside Boeing airplane company accidentally producing a 747 airplane."
15. There are many web pages rebutting Behe's arguments in
detail, including the following:
- Kenneth Miller, "Design on the Defensive",
.
-
Don Lindsay, "Review: 'Darwin's Black Box, The Biochemical Challenge to
Evolution' by Michael J. Behe", August 2000.
-
"Irreducible Complexity and Michael Behe", The Talk.Origins Archive.
16. Michael Behe, Darwin's Black Box (Simon & Schuster, 1998), pp. 39-40.
17. Michael Behe, "Self-Organization and Irreducibly Complex Systems: A Reply to Shanks and Joplin", Philosophy of Science 67 (1), 2000:
Systems requiring several parts to function that need not be well-matched, we can call "simple interactive" systems (designated 'SI'). Ones that require well-matched components are irreducibly complex ('IC'). The line dividing SI and IC systems is not sharp, because assignment to one or the other category is based on probabilistic factors which often are hard to calculate and generally have to be intuitively estimated based on always-incomplete background knowledge. Moreover, no law of physics automatically rules out the chance origin of even the most intricate IC system. As complexity increases, however, the odds become so abysmally low that we reject chance as an explanation (Dembski 1998).
18. Kenneth Miller, "The Evolution of Vertebrate Blood
Clotting".
-
Don Lindsay, "How Could The Immune System Evolve?", April 1999.
-
Mike Coon, "Is the Complement System Irreducibly Complex?", The Talk.Origins
Archive, February 2002.
-
Ian Musgrave, "Evolution of the Bacterial Flagella", March 2000.
An updated version of this web page is currently in preparation.
19. Michael Behe, "Reply to My Critics: A Response to Reviews of Darwin's Black Box: The Biochemical Challenge to Evolution", Biology and Philosophy 16: 685–709, 2001:
It is now clear that, although the mousetrap paradigm remains a good one, there is some ambiguity in the written definition, as discussed below. Nonetheless, I think the definition can be repaired.
20. Michael Behe, "A Response to Critics of Darwin's Black Box", Discovery Institute, December 2001:
Envisioning IC in terms of selected or unselected steps thus puts the focus on the process of trying to build the system. A big advantage, I think, is that it encourages people to pay attention to details; hopefully it would encourage really detailed scenarios by proponents of Darwinism (ones that might be checked experimentally) and discourage just-so stories that leap over many steps without comment. So with those thoughts in mind, I offer the following tentative evolutionary definition of irreducible complexity:
An irreducibly complex evolutionary pathway is one that contains one or more unselected steps (that is, one or more necessary-but-unselected mutations). The degree of irreducible complexity is the number of unselected steps in the pathway.
21. I use the term functional complexity in a loose sense to refer to the sort of complexity which we intuitively recognize when we look at machines and organisms.
22. Dembski quotes Joseph Culberson in a passage which appears to use the term blind search in Dembski's second sense (p. 196). But careful reading of Culberson reveals that he is using the term to mean any black-box algorithm: "The environment acts as a black box, and so we refer to this as the black box or blind search model.... [Wolpert and Macready] prove within a formal setting that all optimization algorithms have equivalent average behavior when pitted against such a black box environment." Joseph Culberson, "On the Futility of Blind Search", Evolutionary Computation 6(2), 1998. An earlier version of the paper can be found online.
23. William Dembski, "Why Natural Selection Can't Design Anything", 2001.
24. Geoffrey Miller, "Technological Evolution As Self-Fulfilling Prophecy", in J. Ziman (Ed.), Technological innovation as an evolutionary process (Cambridge U. Press, 2000). pp. 203-215.
25. David Wolpert and William Macready, "No Free Lunch Theorems for Search", Santa Fe Institute Technical Report 95-02-010, 1995.
26. Since Richard Dawkins' Weasel program will already be familiar to many readers, I will not describe it here. Dawkins' original description can be found in The Blind Watchmaker (Penguin, 1991), pp. 45-50. A brief account can be found online at The Evolution of Improved Fitness By Random Mutation Plus Selection, section 1.2.3. Dembski's description of the program in No Free Lunch contains serious errors.
Dembski also follows in a long line of Creationists and Intelligent Design proponents who have criticized the Weasel program for failing to be something which Dawkins has never claimed it to be. According to Dembski, the program is purported by Dawkins "to show how an evolutionary algorithm can generate specified complexity" (p. 181). In reality, Dawkins neither calls the Weasel program an evolutionary algorithm nor claims that it can "generate" complexity of any sort. The sole purpose of the Weasel program was to illustrate the difference between single-step selection and cumulative selection. (These two terms are described in 6.8 above.) Dawkins is very careful to state this clearly, though apparently not clearly enough for antievolutionists. Dembski quotes the following passage from Dawkins, but appears not to have understood it:
Although the monkey/Shakespeare model is useful for explaining the distinction between single-step selection and cumulative selection, it is misleading in important ways. One of these is that, in each generation of selective "breeding", the mutant "progeny" phrases were judged according to the criterion of resemblance to a distant ideal target, the phrase METHINKS IT IS LIKE A WEASEL. Life isn't like that. Evolution has no long-term goal. [p. 208]
Dembski also presents a revised version of the program, and then makes the absurd claim that his version, unlike Dawkins' original, does not involve an element of "teleology" because it searches the phase space "without explicit recourse to the target" (p. 193). In reality both versions described by Dembski make explicit recourse to the target, comparing each trial sequence against the target sequence.
27. See, for example, Hugh Ross, "Design and the Anthropic
Principle".
For
a refutation of the cosmological fine-tuning argument, see Theodore Drange, "The
Fine-Tuning Argument Revisited (2000)", Philo 2000 (Vol. 3, No. 2).
28. David Wolpert and William Macready, "No Free Lunch Theorems for Optimization", IEEE Transactions on Evolutionary Computation, 1(1):67-82, April 1997.
29. In terms of a computer program, we can think of the fitness function being updated by another module, separate from the optimization algorithm. Because of the black-box constraint, this additional module, representing external factors, is not allowed to communicate with the algorithm module in any other way if we want NFL to apply.
30. Thomas Jansen, "On Classifications of Fitness
Functions", 1999.
See also:
- Stefan Droste, Thomas Jansen and Ingo Wegener, "Perhaps Not a
Free Lunch But At Least a Free Appetizer", Proceedings of the 1st Genetic and
Evolutionary Computation Conference (July 13-17, 1999, Orlando, FL), pages
833-839.
-
Oliver Sharpe, "Beyond NFL: A Few Tentative Steps", Genetic Programming 1998:
Proceedings of the Third Annual Conference (July 22-25, 1998, University of
Wisconsin).
-
Christian Igel and Marc Toussaint, "On Classes of Functions for which No Free
Lunch Results Hold", 2001, submitted to IEEE Transactions on Evolutionary
Computation
31. Dembski establishes a higher-order fitness function F on the phase space Ω × J, where Ω is the original phase space and J is the set of all possible fitness functions on Ω. He then considers a search over this space, i.e. a sequence of ordered pairs (xi, fi), where xi is in Ω and fi is in J, with Fi = fi(xi). Dembski's F is equivalent to the time-dependent fitness function T considered by Wolpert and Macready.28 In Wolpert and Macready's NFL Theorem 2, T is independent of the algorithm, so it cannot take coevolution into account. With coevolution, fi is dependent on the current state of the population.
32. Dembski is inconsistent in his usage of the terms specified information and CSI. Sometimes they are "items" of the form (T, E), where E is an observed outcome and T (or target) is another name for a detachable rejection region R (pp. 142-143). Sometimes they are properties which are either exhibited or not by a phenomenon (p. 151). Sometimes they are quantities: "Because small amounts of specified information can be produced by chance..." (p. 161); "The CSI in a closed system of natural causes remains constant or decreases" (p. 163). To avoid long-winded expressions such as "the quantity of information in an item of specified information" (p. 160), I will use specified information (or SI) in the last of these three senses, i.e. as a quantity. I will use CSI in the second sense, i.e. as an attribute which is either exhibited or not. It should be understood that the probability used in calculating SI or CSI is always the probability of a detachable rejection region R, and not just the probability of the observed outcome E on its own.
33. Thomas Schneider, "Evolution of Biological Information", Nucleic Acids Research, 28(14): 2794-2799, 2000. Also at this site you can find Schneider's response to Dembski's treatment of his work: "Rebuttal to William A. Dembski's Posting and to His Book 'No Free Lunch'", March 9 2002; and a useful "Information Theory Primer".
34. Perhaps Dembski's choice of terminology has helped confuse him. The phase space of an optimization algorithm is normally called a search space, while the phase space of a probability distribution is called an outcome space or sample space. By always using the term phase space regardless of the context, Dembski has blurred this distinction.
35. It isn't clear whether Dembski considers this to be 38 bits of specified complexity/information (SI). He does say that the sequence METHINKS is specified, insofar as it is a "known word in the English language". But, if the specification is "known word in the English language", he needs to calculate the probability of drawing any English word of 8 letters, giving a rather lower complexity value. In fact, Dembski only writes that the complexity is bounded by 38 bits, not that it is precisely 38 bits. Perhaps this was to allow for alternative words of 8 letters.
36. I have found in past discussions of Dembski's work that considerable confusion has been caused by his misuse of Shannon information theory. Although not essential to my critique, I will attempt here to clear up some of this confusion. My main source is The Mathematical Theory of Communication (Univ. of Illinois Press, 1949). This small book consists of two papers, one each by Claude Shannon and Warren Weaver. An earlier (1948) but largely identical version of Shannon's paper is available online. For a more gentle online introduction to information theory, see "Information Theory Primer".
Shannon information theory is concerned with the transmission of messages through a communications channel. The meaning of the messages is immaterial. All that matters is the efficiency and accuracy with which messages are transmitted. Messages are treated as if they were selected at random from an ensemble of possible messages. This means that the same theory can also be used in relation to other types of probabilistic events, in which the occurrence of one outcome is observed out of a set of possible outcomes.
The rate of transmission of information is defined by Shannon as follows:
R = H(x) - Hy(x)
If we think in terms of transmitting a message, drawn randomly from a set of possible messages, from a transmitter to a receiver, then H(x) is the receiver's uncertainty about which message was (or will be) transmitted before receiving any message. Hy(x) is the receiver's uncertainty about which message was transmitted after receiving a message. R can also be thought of as the reduction in uncertainty as a result of receiving the message. If the channel is free of noise--so the message received is always the same one that was sent--then Hy(x) = 0 and R = H(x).
The uncertainty H(x) (or simply H) is defined as follows:
H = - Σi=1...N pi log2pi
where there are N possible messages and the probability of message i being transmitted is pi.
It is important to bear in mind that R and H are rates, or averages (weighted by probability), based on the ensemble of all messages which could possibly be transmitted. They are not values associated with the receipt of one particular message. There is, however, another measure, defined as -log2pi, which is associated with receipt of a specific message. It is sometimes known as surprisal, after M. Tribus [Thermostatics and Thermodynamics (D. van Nostrand Co., 1961)], as it indicates how surprised we should be at receiving that message. The uncertainty H is then equal to the average surprisal, over all possible messages, weighted by probability.
There appears to be some disagreement about which measure is correctly known as the Shannon information. Some writers, including Dembski, refer to the surprisal as the Shannon information associated with the receipt of one specific message. The thinking seems to be that, if H is the rate of transmission of information averaged over all possible messages, then the surprisal must be the information associated with the receipt of one particular message.
However, this is not the usage of Shannon or Weaver, who refer to R as the information. Consequently, most information theorists refer to R as the Shannon information. The expression -log2pi appears nowhere in the Shannon and Weaver papers. For a noise-free channel, Shannon equates information with uncertainty:
The quantity H has a number of interesting properties which further substantiate it as a reasonable measure of choice or information. [Shannon & Weaver, 1949, p. 51]
Weaver is more explicit, and makes it clear that information is a property of the ensemble of possible messages, not of one particular message:
To be sure, this word information in communication theory relates not so much to what you do say, as to what you could say. That is, information is a measure of one's freedom of choice when one selects a message. If one is confronted with a very elementary situation where he has to choose one of two alternative messages, then it is arbitrarily said that the information, associated with this situation, is unity. Note that it is misleading (although often convenient) to say that one or the other message conveys unit information. The concept of information applies not to the individual messages (as the concept of meaning would), but rather to the situation as a whole, the unit information indicating that in this situation one has an amount of freedom of choice, in selecting a message, which it is convenient to regard as a standard or unit amount. [Shannon & Weaver, 1949, pp. 8-9]
Note that, when all the possible outcomes are equally probable (i.e. pi is a constant p) the uncertainty reduces to - log2p:
H = - Σi=1...N pi log2pi
= - N . p log2p
= - N . 1/N . log2p
= - log2p
This must not be confused with the surprisal, although it has the same formula. For an ensemble of possible outcomes which are all equally probable, the surprisal of each outcome just happens to equal the uncertainty of the ensemble.
For the sake of an example, consider a 5-card hand dealt from a well-shuffled deck of 52 cards. There are (52×51×50×49×48)/(5×4×3×2×1) = about 2 million possible outcomes. Since all outcomes are equally probable p = 0.0000005, and the uncertainty (H) associated with the deal is -log2(0.0000005) = 21 bits, using the special formula for equiprobable distributions just derived above. Once we have seen the 5 cards there is no uncertainty about what was dealt, so Hy(x) = 0, and the Shannon information is given by R = 21 - 0 = 21 bits.
Now suppose that, as in Dembski's example (pp. 126-127), a royal flush (10-J-Q-K-A in one suit) is dealt. There are 4 possible royal flushes (one in each suit), so the probability of a royal flush of any suit is 4 × 0.0000005 = 0.000002. The surprisal of this event is therefore -log2(0.000002) = 19 bits.
Like some other writers, Dembski refers to the surprisal (-log2pi) as Shannon information (p. 230n16). This in itself is not particularly important. What matters is not what he calls this measure but how he uses it. The trouble is that he merely uses it as a disguised probability measure. The function f(x) = -log2x is a monotonic function, which means that greater surprisal always corresponds to greater improbability. Every one of Dembski's statements about information could just as well (and with much greater clarity) be expressed as a statement about improbability. He often uses the terms improbability, information and complexity interchangeably. In the index of The Design Inference he even has an entry for "probability... information in disguise". By disguising his probabilities as information, Dembski simply adds another layer of obfuscation to his arguments, without achieving anything of value.
37. Kumar Chellapilla and David Fogel, "Co-Evolving Checkers Playing Programs using only Win, Lose, or Draw", SPIE's AeroSense'99: Applications and Science of Computational Intelligence II (Apr. 5-9, 1999, Orlando, Florida).
38. Strictly speaking, each neural net in a generation has a different fitness function, since its environment (the population of other neural nets) is different.
39. This is pessimistic. A modest overlap of ranges (e.g. W- a little smaller than D+) may still give a good result.
40. Chellapilla and Fogel's scoring regime is the one in which W- = W+ = +1, D- = D+ = 0, and L- = L+ = -2.
41. The algorithmic information or Kolmogorov complexity of a sequence is the length of the shortest program which is able to generate the sequence. It is therefore a measure of incompressibility.
42. Paul Davies, The Fifth Miracle (The Penguin Press, 1998), pp. 85-89.
43. Leslie Orgel, The Origins of Life (Chapman and Hall, 1973), p. 190.
44. Dawkins, on the other hand, does adopt a definition of complexity based on probability under a uniform probability distribution, and perhaps this is where Dembski obtained the idea. In The Blind Watchmaker Dawkins writes:
Let us try another tack in our quest for a definition of complexity, and make use of the mathematical idea of probability. Suppose we try out the following definition: a complex thing is something whose constituent parts are arranged in a way that is unlikely to have arisen by chance alone. To borrow an analogy from an eminent astronomer, if you take the parts of an airliner and jumble them up at random, the likelihood that you would happen to assemble a working Boeing is vanishingly small. There are billions of possible ways of putting together the bits of an airliner, and only one, or very few, of them would actually be an airliner. [Richard Dawkins, The Blind Watchmaker (Penguin, 1991), p. 7.]
Although Dawkins also employs the term specified, it is not clear that his term means the same as Dembski's. Although he is not quite explicit, it seems that Dawkins requires us to consider all functions that the object might have had, and not just the particular function that we observe, as Dembski's concept allows. Furthermore, Dawkins briefly mentions an additional criterion of heterogeneity, which perhaps saves highly patterned phenomena from being classified as complex, as happens with Dembski's version. Dawkins' definition of complexity may be flawed too, but this is relatively unimportant, since he uses it only to clarify what sort of systems he is talking about, and it does not play a significant part in his argument:
I am aware that my characterization of a complex object--statistically improbable in a direction that is specified not with hindsight--may seem idiosyncratic.... If you prefer some other way of defining complexity, I don't care and I would be happy to go along with your definition for the sake of discussion. [Richard Dawkins, The Blind Watchmaker, p. 15.]
45. Richard Dawkins, The Blind Watchmaker, pp. 45-50.
46. The complete list can be found at: William Dembski, "Intelligent Design Coming Clean", Metaviews online forum, November 2000.
47. William Dembski, "Is Intelligent Design Testable?", Metaviews online forum, January 2001.
48. Douglas Theobald, "The Opportunistic Nature of Evolution
and Evolutionary Constraint", The Talk.Origins Archive
-
Chris Colby & Loren Petrich, "Evidence for Jury-Rigged Design in Nature",
The Talk.Origins Archive.
49. For a list of predictions of evolutionary theory,
see:
- Douglas Theobald, "29 Evidences for Macroevolution", The Talk.Origins
Archive, March 2002.
-
Don Lindsay, "Is Evolution Science?", August 2001.
50. Douglas Theobald, "The One True Phylogenetic Tree", The
Talk.Origins Archive.
It
will do Dembski no good to point out that there are a few exceptions to this
congruence. The methods for establishing phylogenetic trees are fallible. The
prediction is only that there will be a high degree of congruence, not perfect
congruence.
51. Beth McMurtrie, "Darwinism Under Attack", The Chronicle of Higher Education, December 21, 2001.
52. The following endorsement appeared on the cover of Dembski's book Intelligent Design: The Bridge Between Science & Theology:
William Dembski is the Isaac Newton of information theory, and since this is the Age of Information, that makes Dembski one of the most important thinkers of our time. His "law of conservation of information" represents a revolutionary breakthrough. In Intelligent Design: The Bridge Between Science & Theology, Dembski explains the meaning and significance of his discoveries with such clarity that the general public can readily grasp them. He convincingly diagnoses our present confusions about the relationship between science and theology and offers a promising alternative.
-- Rob Koons, Associate Professor of Philosophy, University of Texas at Austin
Dembski and Koons are both fellows of the Discovery Institute's Center for the Renewal of Science & Culture, a body which exists specifically for the purpose of promoting Intelligent Design. This sort of mutual puffing of each other's books is commonplace among fellows of the Center.
53. Keith Devlin, "Snake Eyes in the Garden of Eden", The Sciences, July/August 2000.
54. Keith Devlin concurs with this assessment. (Personal communication.)
55. In response to my enquiry on the subject, Sam Northshield (the author of the notice) replied: "The work that I reviewed was, as I remember, definitely more philosophical than mathematical and I judged it as a philosophical work. I don't remember trying hard to understand its math content (either because it seemed difficult to follow or because there was none-- I don't remember which!). Therefore, I can't say anything about the correctness of Dembski's work and my review should not be construed as a mathematical judgement of the work." (Personal communication.)
56. Colin Howson & Peter Urbach, Scientific Reasoning: The Bayesian Approach (Open Court, 1993).
58. Theodore Drange, "The Fine-Tuning Argument (1998)".
59. For a very detailed analysis of observational selection effects, see Nick Bostrom, "Observational Selection Effects and Probability", 2000.
60. Dembski, The Design Inference, pp. 182-183.
61. Howson & Urbach, Scientific Reasoning, pp. 179-180 (quoted by Dembski, The Design Inference, pp. 199-200).
This article first appeared in the Talk.Origins Archive.