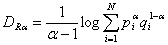
Posted October 15, 2007
In 2004 William Dembski disseminated an article wherein he introduced an allegedly novel measure of information he dubbed "Variational Information." This measure was in fact not a novel quantity but rather a well known (for over forty years) "Rényi divergence of the 2nd order." When his flop was pointed out, Dembski added to his article a reference to Rényi. However, the amended version of Dembski's article contained statements which showed that Dembski not only was not familiar with the widely known and heavily referenced work of Rényi, but did not grasp its essence even after it was pointed out to him. In the three years after the amended version of Dembski's article was posted, Dembski has kept that version posted without any signs of having a second thought. This allows one to think that no self-correction from Dembski is forthcoming. These facts seem to support the opinion of Dembski as being, in the words of Professor Shallit, a "pseudo-mathematician". I similarly suggested that his mathematical exercises are "quasi-mathematics." Contrary to Dembski's claims, it in no way can serve as a "mathematical foundation of Intelligent Design." Although in the opinion of ID advocates it contains innovative and useful stuff, all that is "innovative" there is usually useless, while all that is useful there has usually been known for a long time.
I believe it was a famous French philosopher who said that everybody can make mistakes but only a fool stubbornly adheres to them. The story I am going to tell now may serve as an illustration of the above maxim, with a small modification: although the term "fool" may still (arguably) reflect the situation, the term "incompetent" is applicable unarguably. The hero of the story is William Dembski.
Professor Jeffrey O. Shallit is a well known mathematician and computer scientist, the author of high level mathematical monographs and articles in professional peer-reviewed journals. Naturally when Jeffrey Shallit offers his opinion of the qualifications of authors of publications in various areas of mathematics, it has considerable weight and a good chance of being well thought of and strongly justified. This must be especially true when such an opinion is about the mathematical prowess of somebody who happened to be at some time in the recent past a student in a class taught by Professor Shallit.
The case in point is that of a "leading light" of the intelligent design movement, William A. Dembski, at present time reportedly a research professor of philosophy of religion at a Baptist seminary in Texas, who holds PhD degrees in both philosophy and mathematics. Dembski is considered by ID advocates as the foremost mathematician within their ranks. His colleagues and acolytes incessantly praise in superlative terms Dembski's contribution to ID. [1]
A double doctor (with additional degrees in psychology and religious studies) is supposed to be an expert at least in the fields of his educational specialization, in Dembski's case including mathematics. Oddly, Professor Shallit's professional opinion of Dr-Dr. Dembski seems to be rather unflattering. Indeed, in Dr. Shallit's deposition preceding the famous Dover trial, he unequivocally called Dembski a "pseudo-mathematician." [2]
While I can't speak for other readers of Shallit's deposition, I was not surprised in the least by his low opinion of Dembski as a mathematician. Indeed, in Chapter 1 of my book [3] there is a section wherein I showed Dembski's penchant for loading his texts with esoteric mathematical notations adding nothing to the gist of his discourse and seeming to be a device applied solely for the sake of imbuing his output with a quasi-mathematical appearance (the text of the section in question can also be seen online [4]). It goes without saying that neither Dembski nor any of his supporters has ever admitted the existence of my comments.
Given the high esteem in which Dembski is held in by ID advocates (as illustrated by the references in [1]), they could no more be pleased by Shallit's characterization of Dembski's mathematical exercises than by my comments regarding his mathematically-empty notations-heavy passages. Unfortunately for ID advocates, there is a shortage of mathematicians of Shallit's status among their "theorists." Therefore they largely pretend that Shallit's characterization of Dembski's mathematics does not exist, or at the best let some of their second- and third-tier soldiers evince a supposed rebuttal (often plainly meaningless) of Shallit's work (as in the case of Elsberry and Shallit's devastating skewering of Dembski's concept of "Complex Specified Information" [5]).
It seems to be of a certain interest to look for other evidence, independent of Professor Shallit's or my opinion, which would either support or contradict Shallit's and my view of Dembski as a mathematician. If Shallit and I are right, and the supposed mathematical foundation of ID by Dembski is indeed of no value, this should reflect in a strongly negative way upon the overall credibility of the intelligent design conceptual system.
In view of the above, it seems to be instructive to look at a story that took place in August 2004, when Dembski disseminated an article wherein he claimed to have invented a novel measure of information.
In the original version of his paper (soon afterwards removed from the web but not before it was downloaded and saved by a number of readers) Dembski suggested a supposedly innovative measure of information he dubbed "variational information" (VI).
Almost immediately, responding to Dembski, mathematician Cosma R. Shalizi pointed out [6] that Dembski's VI is nothing more than a particular case of a well known (for over 40 years) quantity known as Rényi divergence.
As a result of Shalizi's comments, Dembski promptly posted an amended version [7] (dated August 12, 2004) of his paper, where he inserted references to Rényi .
Just in case that amended version of Dembski's article one day disappears from the above web location (like the original version did), I have downloaded and saved it.
So far so good -- a mathematician happened to "reinvent the wheel;" such occurrences happen sometimes, and not only with mathematicians -- see for example an essay [8]. It was odd, though, that a supposed expert in this particular field of mathematics was not familiar with rather famous results by a prominent mathematician Alfréd Rényi, widely published and heavily referenced for over forty years.
Since Dembski amended his paper, this could be the end of the story, were it not for an additional quirk.
I am a physicist rather than a mathematician. Nevertheless, I could not fail to notice that the amendment made by Dembski in his article revealed that even after Shalizi pointed to Rényi's result, Dembski still seemed not only to be unfamiliar with an important result in his supposed area of expertise, but also seemed to still simply not comprehend Rényi's work.
For example, in the Abstract that opens the amended version of Dembski's paper, we read, among other things, "The resulting information measure is special case of the Rényi information divergence (also known as the Rènyi entropy)." (emphasis added).
Let us look up definitions of Rényi entropy and of Rényi divergence. Although in August 2004 I verified these definitions by looking up Rényi's own publications, today it seems to be easiest to look up not Rényi's original publications, but just Wikipedia. [9]
Indeed, here they are:
Rényi divergence:
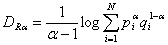
Rényi entropy is however
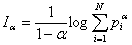
In the above equations α stands for the order of either divergence or entropy; p and q are random variables in two sets with different distributions.
(For continuous distributions these equations are generalized by replacing sums with appropriate integrals).
Even for readers completely unfamiliar with Rényi's work, it is clear just by looking at the above equations that, contrary to Dembski's assertion cited above, Rènyi divergence is not "also known as Rényi entropy," because Rényi divergence and Rényi entropy are two different quantities.
It looks like, even having accounted for Shalizi's critique and thus in fact implicitly admitting his insufficient ken in the area of his supposed expertise, Dembski still has not done his homework fully -- he seems not to realize the difference between the above two quantities, the difference illustrated even in such a commonly accessible source as Wikipedia.
In the original version of his paper Dembski did not at all refer to either of these two quantities, thus creating the impression that he has introduced a novel type of information measure -- variational information. When Shalizi pointed out that "variational information" is nothing more than the Rényi divergence of the order of 2 (i.e. when α =2), Dembski amended his paper but the above quotations from the amended version seem to indicate that he still does not have an adequate grasp of the matter.
Furthermore, in a response to Shalizi's comments, which was posted in 2004 at the ARN website, Dembski tried to downplay the initial lack of references to Rényi . He still maintained that his paper contributed something of substance to information theory. With his typical modesty, Dembski did not hesitate to characterize his own alleged contribution as "admirable."
In particular, Dembski insisted that his paper was innovative because allegedly nobody has ever used Rènyi's measures of the second order. In the amended paper he wrote, "The variational information, though implicit as a special case in the Rényi information divergence (r=2) has to date gone largely unnoticed and unappreciated." (Dembski notation r stands for α in the above equations).
This assertion was not true. For example, in a paper by López-Ruiz [10] it was shown that the quantity introduced by López-Ruiz, Mancini, and Calbet [11] under the name of "disequilibrium" (which happens to be a measure of a divergence of a probability distribution from uniformity, thus functioning as another version of what Dembski suggested as a supposedly novel measure of information) is closely related to the Rényi entropy of the second order, via an exponential term.
Hence, there was little pioneering in Dembski's suggestion of using a second order version of Rènyi measures -- it has been done before. Again, Dembski obviously was not familiar with publications directly related to his supposed area of expertise.
So it seems that the epithet "admirable," suggested by Dembski for his own paper, was not quite adequate for a reasonable evaluation of his own work.
A natural question to ask is why have I waited over three years before going public with the above critique? The answer is simple: not to appear to be eager to pounce upon Dembski at each opportunity; it seemed reasonable to give Dembski a chance to realize his mistakes and to correct them on his own. In the three years since Dembski published his error he has kept his "amended" article posted without any signs of having realized his errors. This allows one to think that no self-correction from Dembski is forthcoming.
This, in turn, allows one to assert that to all intents and purposes Professor Shallit was right in defining Dembski as a pseudo-mathematician and therefore that all the alleged "Mathematical foundation of Intelligent design" so vigorously and triumphantly trumpeted by Dembski and his acolytes, is pseudo-mathematics. It can't serve as a foundation of any reasonable conceptual set. Although in the opinion of ID advocates it contains innovative and useful stuff, in fact all that is "innovative" there is usually useless (like the confusion of Rényi divergence with Rényi entropy), while all that is useful there has usually been known for a long time (like Rényi divergence of the 2nd order).
As has been pointed out more than once, by various authors [12], the "theory" of intelligent design is scientifically empty. Elementary errors, sometimes reluctantly admitted, but more often never admitted at all, are expected even from the best educated ID practitioners like William Dembski, not to mention his lesser admirers and followers.
1. Statements claiming that William Dembski is a first-rank mathematician are common in ID literature. Perhaps the most exaggerated of these accolades was produced by an ID advocate, professor of philosophy Rob Koons in a blurb to Dembski's book "Intelligent Design" (InterVarsity Press, 1999) where Koons referred to Dembski as "the Isaac Newton of information theory," and "one of the most important thinkers of our time." Michael Behe, in the foreword to the same book by Dembski, claimed that the future development of science will be based on design and hence on the "theoretical foundation of Bill Dembski's work." (page 12 in Dembski's book). Similar assertions can be found in the publications of many other ID advocates.
2. Shallit, Jeffrey O. "Expert Report under Federal Rule of Civic Procedure 26." (See http://www2.ncseweb.org/kvd/experts/shallit.pdf Accessed on Oct. 6, 2007.
3. Mark Perakh, Unintelligent Design. Prometheus Books, Amherst, NY 2003 (pages 26-28).
4. Mark Perakh. "A Consistent Inconsistency." in Talk Reason (see http://www.talkreason.org/articles/dembski.cfm). Accessed on October 6, 2007
5. Elsberry, Wesley R and Jeffrey O. Shallit., "Information Theory, evolutionary computation, and Dembski's complex specified information" (see http://www.talkreason.org/articles/eandsdembski.pdf). Accessed on Oct. 6, 2007.
6. Shalizi, Cosma R. "William Dembski and the Discovery Institute, Renewing Science and Culture by Re-Inventing the Wheel." (See http://www.cscs.umich.edu/~crshalizi/weblog/234.html). Accessed on Oct. 6, 2007).
7. Dembski, William A. "Information as a Measure of Variation". (See http://www.iscid.org/boards/ubb-get_topic-f-10-t-000086.html). Accessed on Oct. 6, 2007).
8. Perakh, Mark. "Reinventing the wheel." In Talk Reason (see http://www.talkreason.org/articles/wheel.cfm). Accessed on Oct. 6, 2007.
9. Wikipedia article on Rényi quantities is found here: http://en.wikipedia.org/wiki/R%C3%A9nyi_entropy.
10. López-Ruiz, Ricardo. "Shannon Information, LMC complexity and Rényi entropies: a straightforward approach" (See http://arxiv.org/PS_cache/nlin/pdf/0312/0312056.pdf), Dec 22, 2003.
11. López-Ruiz, R., H. L. Mancini, and X. Calbet. "A Statistical Measure of Complexity." Phys. Lett., A209, 321-326 (1995)
12. Critique of Dembski's output, including his mathematical exercises, is found in multiple publications, including the above referenced Shallit's deposition (ref. 2), Elsberry-Shallit's essay on Complex Specified Information (ref. 5), posts by Richard Wein and other authors on Talk Reason website (http://www.talkreason.org/), posts on Mark Chu-Carroll's blog "Good math bad math," many posts on The Panda's Thumb blog (http://www.pandasthumb.org), in my book (ref. 3) as well as in the book by Niall Shanks, (God, the Devil and Darwin, Oxford Univ. Press, 2004); in the anthology Why Intelligent Design Fails, (eds Matt Young and Taner Edis, Rutgers Univ. Press, 2004) and many other sources (many available via Amazon online bookstore).
Matt Young, Paul Gross, and Wesley Elsberry provided helpful comments on the draft of this essay, which are appreciated.